zawy12 / difficulty-algorithms Goto Github PK
View Code? Open in Web Editor NEWSee the Issues for difficulty algorithms
License: MIT License
See the Issues for difficulty algorithms
License: MIT License
This shows the similarity of all difficulty algorithms.
T = target solvetime
n = number of blocks in averaging
r = a dilution aka tempering aka buffering factor
w = a weighting function based on n. It's 1 for all but LWMA. In LWMA it increases from 1 to n from oldest to more recent blocks, giving them more weight.
target = avg(n targets) / r * [(r-1) + sum(n w*STs)/sum(n w's) / T]
Less accurately:
difficulty = avg(n Ds) * r / [ (r-1) + sum(n w*STs)/sum(n w's) / T ]
For clarity, here it is w=1 (no increased weight given to more recent blocks like LWMA and OSS)
target = avg(n targets) / r * [(r-1) + avg(n STs) / T]
w=1, r=1 Dark Gravity Wave (a Simple Moving Average in deep disguise)
w=1, n=1 for EMA. Larger r means smoother, slower response. Other articles show this is almost precisely ASERT (BCH) & ETH's.
w=1, r=4 for Digishield, r=2 for Grin
r=1, w = function of n. LWMA for linear increase in w for more recent blocks. Pretty close to EMA.
r = 4, and simple w function. OSS (like a combination of LWMA and Digishield)
There is not a real-time clock in cryptocoins that has an accurate time except for the median time of node peers (or of just single peers). This puts an upper limit on what time a miner can assign to a block. This upper limit is crucial. If it were not there, miners could assign a large future time which would drive difficulty down as far as they want in only 1 block.
Allowing miners to assign the timestamp instead of simply using the median of node peers is crucial to a cryptocoin. At the core of why POW is used, miners perform a timestamp service as a for-profit competitive group that prevents the need for a 3rd party centralized timestamp service. It can't be accomplished by just nodes in an asynchronous network, especially if many nodes can be created to perform a Sybil attack.
The best way to handle bad timestamps is to make sure the future time limit allowed by nodes is restricted to 6xT or less. Default is on many coins and it is 7200 seconds.
[ Update: to minimize profit from bad timestamps, I am recommending FTL be set to 300 or TxN/20, whichever is larger. ]
A bad timestamp can lower difficulty by N/(N+7200/T) when the future_time_limit is the usual 7200 seconds (Bitcoin and Monero clones). The next honest timestamp will reverse the effect. To maximize the number of blocks a big miner can get without difficulty rising, he assigns to all his blocks
timestamp = (HR+P)/P*T + previous_timestamp
where P is his hashrate multiple of the network's hashrate HR before he came online. For example, if he has 2x network hashrate, he can assign 1.333xT plus previous timestamp for all his timestamps. This prevents difficulty from rising, keeping it the same value, maximizing the number of blocks he can get. With CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT=7200 and T=120 seconds, this would allow him to get 7200/120 = 60 blocks without the difficulty rising. He can't continue because he will have reached the future time limit that the nodes enforce. He then leaves and difficulty starts rising (if negative solvetimes are allowed in the difficulty calculation). If negative solvetimes are not allowed, he gets 60 blocks all the same over the course of 90 blocks that he and the rest of the network obtained. The average real solvetime for the 90 would be 1/3 of T (if he has 2x the network hashrate) without the difficulty rising. And when he leaves, difficulty will stay the same. So the algorithm will have issued blocks too quickly without penalizing other miners (except for coin inflation which also penalizes hodlers).
A miner might be able to own the local node peers and have control of the time limit, but I believe this risks splitting the chain or causing other nodes to reject the blocks.
[update: Graft had big problem from a big miner "owning the MTP". This was made easy by Graft not lowering the FTL from 7200 to 500. Here's a full discussion. ]
The lower limit is approximately 6xT into the past (in Bitcoin and maybe vast majority of all others). It's not based on real time, but on the median of the past 11 block timestamps, which is the 6th block in the past if the 11 blocks had sequential timestamps. This is called median time past (MTP).
The lower limit can get "owned" by a >50% miner who would generally get 6 of the 11 past blocks. He could keep assigning the same time initial_timestamp - 6xT to all his timestamps. By his 7th block it could be -12xT compared to real time because he owns the MTP. Six blocks later he can assign -18xT, and so on. This drives difficulty up (if negative solvetimes are allowed in the difficulty calculation), so its a malicious attack that does not help him.
If an algo has a limit on the rate of difficulty falling that is less strict than its limit on rising (asymmetrical limits) and if it is looking at individual timestamps and allowing negative solvetimes, then he can ironically drive difficulty down by constantly assigning reverse timestamps (it's ironic because a reverse timestamp should send difficulty up). The extreme asymmetry is not allowing negative solvetimes by using if (solvetime<1) { solvetime=1;}. A bad actor with >50% hash rate and constantly assigning negative timestamps in this case would cause difficulty to drop to zero.
[this was written before I realized lowering FTL would solve all timestamps problems]
The +12xT and -6xT limits on timestamps in Bitcoin are pertty good if T=600. In a simple moving average (SMA), an incorrect time that is 12xT into the future would make the difficulty drop for only 1 block by about N/(12+N) which is 17% for a typical N=60. The next block after it would immediately correct the error with a timestamp that is about -11xT his timestamp which should still be a full 6xT ahead of the MTP. Conversely, bad -6xT timestamps would typically raise difficulty less by N/(N-6) and be immediately corrected on the next honest timestamp.
Doing nothing could cause a serious problem for the WHM-like algorithms that give a higher weight to more recent timestamps. If the two most recent blocks are assigned the -6xT, there are many scenarios where difficulty would come out negative, causing a catastrophic problem. It becomes a lot harder to do as N gets higher.
The EMA difficulty would shoot up exponentially in a single block with a single negative solvetime that results from an out-of-sequence timestamp.
Even the SMA could have a problem if N is really low like N=10. For example, if 6 of the past 11 solvetimes were 1xT to allow a -6xT and then if 3 of the 10 in the window were 0.1xT then the denominator will be
5xT+4x0.1xT-1x6xT = -0.6xT
which gives a negative difficulty.
But the worst that can happen in an SMA is if a dishonest 12xT forward stamp is at the end of the window when a -6xT comes in the front, then the difficulty is incorrectly lowered by N/(N+18) and the vice versa case is a rise in difficulty of N/(N-18).
An attacker could also cause a divide by zero failure, or give a really small value for the denominator like 0.001, sending the difficulty up 1000x, effectively forcing a fork.
In DAs that loop over each block in the N window to get all solvetimes rather than subtracting oldest from the most recent timestamp, simply blocking a negative solvetime as in the following code has an ironic catastrophic failure:
if ST < 0 then ST=0
# or this would be about the same
# if ST < 1 then ST=1The failure occurs if a largish ~20% miner keeps assigning the -6xT limit. The irony is that you expect -6xT to drive D up, but since it is converted to 0 second, the next honest timestamp that is solved in a normal 1xT will cause a very large "calculated" solvetime of 7xT for the next block after the biggish miner assigns -6xT. Consider the following timestamps and calculated solvetimes from the loop in an SMA that uses ST= timestamp[i] - timestamp[i-1] when a 20% miner (20% of blocks) assigns -6xT:
apparent solvetimes = 1, 1, 1, -6, 7, 1, 1, 1, -6, 7, 1, 1, 1, -6, 7 (average is 1, so it's OK)
after blocking negatives = 1, 1, 1, 0, 7, 1, 1, 1, 0, 7, .....
When blocking negatives the average ST is 2, so a 20% miner can cut difficulty in half in just 1 window length. When the difficulty drops, more mining will come on and the 20% miner's effect will be reduced. But if he were able to maintain 20%,, difficulty would drop to zero in a few N windows (replace the 1's in the last 2 sequences above with 0 to represent everyone solving in 0 seconds, and the difficulty will still continue to drop).
The EMAs and WHM algorithm would be affected about the same.
For an SMA algo or Digishield v3 who simply subtract the oldest from the newest timestamp to get sum(STs), and is not using MTP as the newest block it is not too bad and a little better than doing nothing. The difficulty could be incorrectly high or low from bad timestamps by N/(N +/- 13) in the case where -6xT is the oldest block in the window and -6xT is also the 2nd to most recent block, causing the most recent block to be +7xT.
This method is if you are not going to allow a signed integer for solvetime (otherwise use method 6). It's good for all algorithms. Method 6 is more accurate and retains symmetry and is preferred.
Superficially it seems like method 2 because the bad timestamp will be reported with a solvetime of zero, but it does not have the catastrophic exploit.
In code it can be done like this:
# Idea from Neil (kyuupichan)
# in case several negatives were in a row before our N window:
# numbering is "blocks into past", -1 = most recently solved block
# The next line could have been just -N-1, but checking more reduces potential small error.
prev_max = max(timestamp[-N-1],timestamp[-N-2],timestamp[-N-3],timestamp[-N-4])
for i=-N to -1
max_timestamp = max(timestamp[i], prev_max)
solvetime[i] = max_timestamp - prev_max
prev_max = max_timestamp
.....
For N in a low range like N=60 combined with a coin that allows timestamps up to 24xT ahead of median of peer node time, the above allows an exploit for getting 15 blocks at ~35% below average difficulty (see further below). The following is a fix for WHM (and WT-144) that retains the above idea, but greatly blocks the exploit without slowing the ability of the difficulty to drop with normal speed if hashrate goes to, say, 1/3.
for i=-N to -1
prev_max_timestamp = max(T[i-1],T[i-2],T[i-3],T[i-4],T[i-5],T[i-6],T[i-7] )
solvetime[i] = T[i] - prev_max_timestamp
if solvetime[i] > 7*T then solvetime[i] = 7*T
...
In EMA's we do it similarly:
L = 7 # limits forwarded stamps
maxT=timestamp[height-7-1]
for ( i = height - 7 to i < height ) { maxT = max(maxT, timestamp[i]) }
ST = timestamp[height] - maxT
ST = max(T/200,min(T*7, ST))
The 7 is chosen based on being a fairly rare event, but also fairly tight choice so that N for the EMA-JE can be N=40 without causing a big problem.
Describing the problem if limit=7 is not used: imagine solvetimes are all magically 1xT in order to simplify the math. Now say a 20% miner comes on and always assigns the max allowed timestamp:
Timestamps:
1,2,3,4,(5+12),6,7,8,9,(10+12)...
Solvetime without using the "7"
1,1,1,13,0,0,0,0,5,0,0,0,0,5,..repeat
Ignoring the 4 startup blocks, avg ST is 1 like it should be. The SMA (with a loop), WHM, and EMA-JE with N=60 (which is like EMA-Z with N=30) all end up at about 22% below the correct difficulty for as long as the miner does this. The 13 triggers a 30% drop in EMA and WHM (18% in SMA) and the 5's slow its recovery. The 5's are actually 4 in the steady state because the difficulty dropped. They are even lower because low difficulty attracts more hash power, so steady state is not as bad as I've said. My point is that there is a recovery in 30 blocks, but there are 15 blocks obtained at an average of 25% too low in WHM and EMA and 15% in SMA.
Monero clones may allow +24xT timestamps and with WHM N=60, this is a disaster. My testing indicates about 25 blocks at 35% below correct difficulty in WHM and EMA-JE with N=60 (EMA-Z N=30). Some clones of other coins may keep a rigid 2 hour max while reducing the T, so that a T=120 seconds coins with a 2-hour max ahead of the median of node peer time would allow a +60xT.
Here's the scenario with the limit=7 protection, assuming the worse situation where +24xT is allowed:
timestamps:
1,2,3,4,(5+24),6,7,8,9,(10+24),11,12,13,(14+24)..
solvetimes with "7" protection:
1,1,1,8,0,0,0,0,5,0,0,0,0,5...
For WHM and EMA, there are 15 blocks obtained at only 15% below the correct difficulty. So it's better under worse circumstances.
The way the 7 is used above "retains symmetry". It limits the jump which makes a smaller N more palatable in the presence of timestamp manipulation. "Retaining symmetry" means it will come back down to the correct value. Making the 7 smaller in the loop than in the max limitation enforced at the end would have caused the difficulty to be below the correct value for a few blocks.
In the algos I've refined the above idea to make the "7" range from 5 to 9. Really, using 5 is problematic it's need to prevent a 20% in an N=40 algorithm every time there's a bad timestamp. So Method 6 is really preferred.
An SMA that simply subtracts first and last timestamps in the window and nothing else would again have much less error in D from bad timestamps, limited to even less than method 2. In this case: N/(N-1) is the max of raising difficulty to N/(N+13) = 18% drop for N=60 for one block (it then immediately corrects when an accurate timestamp comes in). Then when that block exists the window, D rises by 18% for 1 block. so it seems like doing nothing works really well, but method 4 is a way you can prevent the single-bad-timestamp cases from having an effect if you don't mind delaying your response by 1 block: See method 4.
There is another way to stop the single case in SMA's (that subtract first from last timestamps). They could use something like the limit=7 idea and apply it to both the beginning and end of the window to protect as the bad time comes into and out of the window. EMA and WHM don't give hardly any weight when it leaves their "window", so it's not needed there. Here it is for just 4 blocks.
# numbering is "blocks into past"
begin_timestamp =max(timestamp[-N-1], timestamp[-N-2], timestamp[-N-3], timestamp[-N-4] )
end_timestamp = max(timestamp[-1], timestamp[-2], timestamp[N-3], timestamp[N-4] )
total_solvetime = end_timestamp - begin_timestamp
I learned this from BCH's new DAA. For SMAs that subtract first and last timestamps, do this:
begin_timestamp =median(timestamp[-N-1], timestamp[-N-2], timestamp[-N-3] )
end_timestamp = median(timestamp[-1], timestamp[-2], timestamp[N-3] )
I can't logically justify this because it only protects against single bad timestamps when they would not cause much problem anyway and delays response by 1 block. But I love it for some reason, and it inspired the last part of method 3.
You can put symmetrical limits on difficulty changes from the previous block. There's no reason to do this, but I wanted to mention it. I think it's not hardly different than method 6. This is what MANY coins should have used instead of copying Digishield's POW limits that are useless and cause harm if you try to make Digishiled respond faster. This allows the algorithm to change as fast as it can in the presence of a specified-size hash attack starting or stopping, but not faster.
D = calculated D for next block to be considered for limiting
X = 10 # max expected size of "hash attacks" as multiple of bash hash rate
limit = X^(3/N) # 3 for WHM and EMA. Use 2 for SMA
if ( D > prev_D*limit) { D=prev_D*limit }
if ( D > prev_D/limit) { D=prev_D/limit }
Or it can be made to act as if method 6 timestamp limits are in place.
limit = 1+max_allowed_solvetime/N
if ( D > prev_D*limit) { D=prev_D*limit }
if ( D > prev_D/limit) { D=prev_D/limit }
This is the best method if the future time limit determined by median of nodes is not reduced as described at very top.
When a bad timestamp comes through, it can be allowed it to "do its damage" with almost no problem as long as negative solvetimes are allowed. If a forward time is used to try to lower difficulty, the next accurate timestamp that comes through will erase its effect completely in all algorithms. And vice versa if a bad reverse timestamp comes in. Monero clones may allow a 24xT forward time to come in and if the algo uses N=24, then difficulty can be cut to 1/4 in the next blockwhen using the low N's I recommend for T=600 second coins. It can even throw a negative in EMA-Z A limit of 8xT as max solvetime after previous timestamp did not hurt performance much (see chart below). If the limits are not symmetrical, an exploit is possible. If you're using an SMA or Digi v3 for some reason, keep in mind the effects are reversed when the bad timestamp leaves out the back of the window.
if ST > 6*T then ST=6*T
if ST < -5*T then ST= -5*T
Limiting the solvetime makes D slower to drop if there is a big decrease in hashrate. The plots below show what happens without and then with the 8xT limit when hashrate drops to 1/50th with the EMA-Z. This shows performance is not hurt much.
This shows the benefit in a live coin of allowing the negative solvetimes. Graft was using method 3, which is the second best method.
If there was good real-time clock such as all nodes keeping a good universal time, we could theoretically make the network synchronous like a computer relying on a clock pulse and do away with consensus. Synchronous networks do not have FLP or Byzantine problems because there is no need for consensus. In short, every node would have a good universal clock accurate to within a few seconds, and there would be an agreed-upon clock cycle with an "on time" when new transactions are accepted by nodes, and an "off time" to wait for all nodes to get and validate all transactions. It takes about a minute for 0.5 MB blocks to propagate to 90% of nodes, so the off time might need to be 5 minutes. All nodes would accept all valid transactions within the window, but they have to each independently determine what the acceptable window is by their independent but accurate clock (independent so they all do not all use the same source for time which would be an attack-able 3rd party). Then transactions would be sorted into a block and hashed like a regular block chain. Nodes do not theoretically need to ask other nodes anything. They just share transactions. There are hairy details (such as straggling transactions on the edges of the "on window" and re-syncing to get the right block chain when rejoining the network) that would require some asking of other nodes which is the beginning of trusted peers or consensus that only POW has solved. But CPUs work without consensus and with "large" (nanosecond) delays. To what extent are nodes not like a disparate groups of transistors on a CPU waiting on electrons (transactions) to arrive? Nodes going online and dropping out is like only some of the transistors turning off and on, so the analogy even works to show the problems.
Best algorithm:
WHM difficulty algorithm
I've been careful to select the best N and adjustment factor (to get the correct average solvetime) for this algorithm. The next two algorithms are very nearly as good, but the selection of N and adjustment factor are only optimal for T=120 second target solvetimes.
A close 2nd with a lot less code:
Simple EMA difficulty algorithm
Improved version of Digishield has more stability than Simple EMA, but is a little slower. The Simple EMA page shows how to model the EMA to be more like Digishield in order to give what seems to be the same results.
A more advanced form of the Simple EMA, with no advantage other than being more precise. This article also covers every aspect of EMAs.
EMA-Z
New algorithm that might be better but is more complicated:
Dynamic EMA difficulty algorithm
This idea could solve a lot of problems, but bad timestamps arguably prevent it from being better because they force us to require a certain minimum number of blocks, which severely limit it where it is most needed.
Extending EMA algorithm to a PID controller so you can tweak it to have characteristics very different from other algorithms. But overall, it seems to not be adjustable to anything better than the EMA, just different.
PID controller difficulty algorithm
Masari coin (Monero clone) has implemented the WHM N=60 and so far appears to be an incredible success.
See also
Selection of N (more important than choice of algorithm)
Introduction to difficulty algorithms
Comparing algorithms,
Handling bad timestamps.
Difficulty performance of live coins
Hash attack examples
Dark Gravity Wave problems:
2 and 3 cause solvetime to be 6% longer than expected.
# Simple moving average difficulty algorithm
# timestamps[1] = most recent timestamp
next_target = average(N past targets) * (timestamps[1]-timestamps[N+1])/(N*desired_block_time)
Instead of average of past N targets, DGW does this:
# Dark gravity wave "average" Targets
avgTarget = Target[1];
for ( i=2 ; i <= N; i++) {
avgTarget = ( avgTarget*i +Target[i] ) / (i+1) ;
}
There's nothing in the comments to explain what this is supposed to be doing, so I expanded it out for i =2 to 4 (N=4). Target[1] = T1 = previous block's target and T4 is 4th block in the past.

which simplifies to:

This is just an average that gives double weight to the most recent target.
Here's the actual code.
for (unsigned int nCountBlocks = 1; nCountBlocks <= nPastBlocks; nCountBlocks++) {
arith_uint256 bnTarget = arith_uint256().SetCompact(pindex->nBits);
if (nCountBlocks == 1) {
bnPastTargetAvg = bnTarget;
} else {
// NOTE: that's not an average really...
bnPastTargetAvg = (bnPastTargetAvg * nCountBlocks + bnTarget) / (nCountBlocks + 1);
}
if(nCountBlocks != nPastBlocks) {
assert(pindex->pprev); // should never fail
pindex = pindex->pprev;
}
}
And what it should be:
for (unsigned int i = 1; i <= nPastBlocks; i++) {
arith_uint256 bnTarget = arith_uint256().SetCompact(pindex->nBits);
bnPastTargetAvg += bnTarget/nPastBlocks; // simple average
pindex = pindex->pprev;
}
The problem is that there is a sweet spot in attacking, shown here:
==================
Come back to check before doing any pull or merge. Code compiles and is currently on 2 to 5 testnets. Hopefully the testnets will concur with my spreadsheet today 5/22/2018.
Change history:
5/21/2018:
5/22/2018:
There were some instances where LWMA was not performing optimally see LWMA failures. This is an attempt to solve the problem. Large coins should use the Simple EMA. This one should be the best for small coins. This supersedes LWMA, D-LWMA, and Dynamic EMA.
// Cryptonote coins must make the following changes:
// const uint64_t CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT = 3xT; // (360 for T=120 seconds)
// const size_t BLOCKCHAIN_TIMESTAMP_CHECK_WINDOW = 11;
// const unit64_t DIFFICULTY_BLOCKS_COUNT = DIFFICULTY_WINDOW + 1
// Make sure lag is zero and do not sort timestamps.
// CN coins must also deploy the Jagerman MTP Patch. See:
// https://github.com/loki-project/loki/pull/26#event-1600444609
Slipstream EMA Description
Slipstream EMA estimates current hashrate in order to set difficulty to get the correct solvetime. It gives more weight to the most recent solvetimes. It is designed for small coin protection against timestamp manipulation, hash-attacks, delays, and oscillations. It rises 10% per block when an attack begins, so most attacks can't benefit from staying on more than 2 blocks. It uses a very fast Exponential Moving Average to respond to hashrate changes as long as the result is within a +/- 14% range around a slow tempered Simple Moving Average. If it goes outside that range, it switches to a medium-speed EMA to prevent it from rising too high or falling too far. Slipstream refers to it having a strong preference to being "behind" the SMA within +/- 14%. It resists going outside that range, and is anxious to return to it.
// Slipstream EMA difficulty algorithm
// Copyright (c) 2018 Zawy
// EMA math by Jacob Eliosoff and Tom Harding.
// https://github.com/zawy12/difficulty-algorithms/issues/27
// Cryptonote-like coins must see the link above for additional changes.
// Round Off Protection. D must normally be > 100 and always < 10 T.
// This is used because some devs believe double may pose a round-off risk.
double ROP(double RR) {
if( ceil(RR + 0.01) > ceil(RR) ) { RR = ceil(RR + 0.03); }
return RR;
}
difficulty_type next_difficulty(std::vector<std::uint64_t> timestamps,
std::vector<difficulty_type> cumulative_difficulties, size_t target_seconds) {
// After startup, timestamps & cumulative_difficulties vectors should be size N+1.
double T = target_seconds;
double N = DIFFICULTY_WINDOW; // N=60 in all coins.
double FTL = CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT; // < 3xT
double next_D, ST, D, tSMA, sumD, sumST;
// For new coins height < N+1, give away first 4 blocks or use smaller N
if (timestamps.size() < 4) { return 100; }
else if (timestamps.size() < N+1) { N = timestamps.size() - 1; }
// After startup, the following should be the norm.
else { timestamps.resize(N+1); cumulative_difficulties.resize(N+1); }
// Calculate fast EMA using most recent 2 blocks.
// +6xT prevents D dropping too far after attack to prevent on-off attack oscillations.
// -FTL prevents maliciously raising D. ST=solvetime.
ST = std::max(-FTL, std::min(double(timestamps[N] - timestamps[N-1]), 6*T));
D = cumulative_difficulties[N] - cumulative_difficulties[N-1];
next_D = ROP( D*9*T / (8*T+ST*1.058) );
// Calculate a 50% tempered SMA.
sumD = cumulative_difficulties[N] - cumulative_difficulties[0];
sumST = timestamps[N] - timestamps[0];
tSMA = ROP( sumD*2*T / (N*T+sumST) );
// Do slow EMA if fast EMA is outside +/- 14% from tSMA. 0.877 = 1/1.14.
if (next_D > tSMA*1.14 || next_D < tSMA*0.877) {
next_D = ROP( D*28*T / (27*T+ST*1.02) );
}
return static_cast<uint64_t>(0.9935*next_D);
}
Notice how much higher Digishield goes, causing delays.
I'm against a dev such as myself selecting any constant in difficulty algorithms. It should be an objective setting. But due to the non-linearity of of miners jumping on or off based on some rough threshold (like +/- 25%), and based on miners being able to change behavior when the algorithm can't, it's mathematically difficult to develop an algorithm that can figure out the best settings. It seems to need a an A.I. Lacking the skill, I've needed to rely on experience and observation to choose several settings. These are supposedly close to what an A.I. would conclude Some of the constants are not chosen by me other than to do the correct math, but the important ones are. The important ones are 6xT ,+/- 14%, N=60, 50%, N=28, and N=9.
subtitle: My White Whale
Pre-LWMA
In 2016 I worked on trying to improve Zcash's difficulty algorithm with many different ideas. Nothing came of it except for wasting @str4d and @Daria's time. During this time I posted an errant issue to Monero recommending a simple moving average with N=17. It was errant because N=17 was much too fast which also means it randomly varies a lot. It attracts constant on-off mining by dropping 25% too low on accident all day, everyday. Karbo coin adopted it to stop terrible delays resulting from the 24-hour averaging of the default cryptonote algorithm. It saved their coin, they were grateful, and other coins noticed. I found out about Karbo 6 months later when Sumo had to fork for the same reason, adopted it with minor modifications, and contacted me. Karbo had asked for help earlier, but I was busy and didn't respond. Then more CN/Monero/Forknote/Bytecoin clones noticed and copied either Sumo and Karbo. It was known as Zawy v1 but it was no more than a simple moving average. At the time we were not aware that it was not as good as the Digishield Zcash adopted.
Karbo kept me interested in difficulty algorithms in early 2017, testing every idea I had, showing interest, and providing a bouncing board. I was unable to find anything better than a simple moving average, but I learned how to identify good and bad algorithms. BCH (after their EDA disaster) used a good simple moving average seemingly based on my inability to find something better and may have called it my idea, but it's just BTC's algo converted to a rolling average and a much smaller N. They chose N=144 instead of my N=50 and it has worked good for them. They used a symmetrical limit I promoted and devised an interesting median of 3 method (@deadalnix?) for ignoring single bad timestamps at a cost of a 1-block delay.
LWMA discovery
In July 2017, @dgenr8 showed me his WT-144 being tested for BCH that used an LWMA in difficulty. My Excel spreadsheet "difficulty algorithm platform" immediately declared it a winner. I had tried it in 2016 and 2017 on difficulty/solvetime values to get next_difficulty and it didn't work. He applied the LWMA function to solvetime*target values to get next_Target. I see his sound logic in doing it on those values (each target corresponds to each solvetime, so keep them together), but in trying to understand why his
nextTarget = LWMA(STs*targets) / T (ST = solvetime, T=target solvetime)
was so much better than my old testing of
nextDifficulty = LWMA(difficulties/STs) * T
I thought a lot about averaging and came to believe the following should be better:
nextTarget = avgTarget*LWMA(STs) / T
which is the same as
nextDifficulty = harmonicMeanDifficulties/LWMA(STs) * T
Testing revealed this to be just enough better (not greatly, but measurably) that I abandoned WT-144.
Dgenr8's method made me realize simple moving averages like this
next_Target = average(ST)\*avg(target)/T
work better and are more precise than
next_Difficulty = avg(D) * T / avg(ST) * 0.95
Intuitively speaking it should have been more clear because the STs vary a lot, hitting a lot of solvetimes below the average and small values in denominator cause big changes. The 0.95 is a correction factor for N=30 to get the correct solvetime and it gets small as N increases, nearing 0.99 at N=100. The effect is more clearly seen in a different way. This: next_D = T*avg(D/ST) gives terrible results but this next_D = T/avg(ST/D) gives perfect results. The first is avg(1/X) while the 2nd is the correct 1/avg(X). BTW, 1/avg(1/D) = harmonicMean(D).
EMA Discovery
@jacob-eliosoff noticed our work on trying to get BCH a new DA and suggested a specific type of EMA. He seemed to derive it from past experience and intuition in an evening or two and maybe solidified his thinking from a paragraph in Wikipedia's moving average article that seems to have been there only by chance. It always gives perfect solvetimes with any N, so it's the best theoretical starting point. Dgenr8 suggested I try to combine it with an LWMA but I didn't try it because I could see it looked already to be about the same thing, just exponential instead of linear. Dgenr8 then did it himself, and it came out to be almost exactly the same (to our surprise) but his version could handle zero and negatives. He had basically inverted it and come up with something that has deeper theoretical significance if not a little more accuracy. It was yet again showing working in terms of target is mathematically more correct than working in terms of difficulty.
The EMAs do not do as well LWMA in my testing. One thing that makes LWMA shine is its ability to drop quickly after a hash attack. The only avenue for improving difficulty algorithms is to somehow getting one to rise as quickly as the LWMA falls without causing other problems. There are ways to do better but would require substantial changes (such as @gandrewstone's idea to allow difficulty to fall if a solvetime is taking too long and Bobtail that collects the best hashes for each block, not just one, originally for reasons other than difficulty). [ update: I went full throttle on andrewstones idea, making symmetrically and theoretically perfect with EMA. See "TSA article" ]
The EMA is better than the original LWMA but not quite as good as the new one. Jacob recommended using the EMA because it could be simplified with an e^x = 1 + x substitution in addition to not needing a loop. I opted to "advertise" the more complicated LWMA. I wanted to be sure we had the best for small coins, especially in its ability to drop after an attack. After showing them the results of a more complicated Dynamic LWMA, devs already aware of complexity problems want me it anyway (it switches to smaller N during hash attacks).
I found a section in a book that briefly described how to use the EMA as a PID controller and employed it. This is something many people have considered. But, as I expected for theoretical reasons, it could only do as well as our other algorithms, not better. But like the others, it acts in its own interesting way.
The Stampede for LWMA
After Masari rapidly forked to be the first to implement LWMA in early December 2017, there was a stampede to get it to stop new catastrophic attacks that were occurring from Nicehash if not ASICs that people were not yet aware of. Zawy v1 was no longer sufficient protection as the oscillations all day were bad. Bigger coins on the default CN algo were beginning to find it as unacceptable as the smaller coins always had. Now (5 months later) there are over 30 coins who have implemented LWMA or are about to. About 1 coin per 3 days is getting it.
History of LWMA issues & improvements
Masari was in a rush and therefore did not want to redo variable declarations to allow negative solvetimes. @thaer used if ST < 1 then ST =1 which allows a catastrophic exploit. After seeing this in his code, I immediately showed him @kyuupichan's (?) method of handling out-of-sequence timestamps. Two weeks later he forked to do the repair. Unfortunately, other coins had copied his initial code without us knowing it which led to catastrophic exploits with one coin losing 5000 blocks in 2 hours.
Cryptonote coins sometimes kept old Cryptonote code that caused problems. One problem was a sort of the timestamps before LWMA was applied which is a milder form of the problem above. Another problem was keeping in the 15 block lag which is basically a 15 block gift to an attacker, making LWMA seem slow to respond. Cut should also be changed to zero.
Several coins did not change their N. It appears they just briefly read about it and forked to implement it. One used N=17 left over from Karbo and Sumo. Another left N = 720 from CN default. Another used N=30. All of these were clearly not as good as the recommended N =~ 60.
In December I told BTG about there not being any fix to > 50% miners who apply a bunch of forwarded timestamps. My +7/-7 limits in the code only stopped < 50% bad timestamps. I then realized the FTL could be lowered to stop even > 50% attacks from causing harm. I started telling LWMA coins to lower their FTL and shortly thereafter the first attacks using bad timestamps on coins who had not changed the FTL began. They all had to fork ASAP to correct it. Some have not. Coins copying others' LWMA without changing their FTL is a continuing threat.
IPBC copied my recommended LWMA code which was a Karbo version with some variable declaration problems corrected by Haven. IPBC's testnet ran fine. But like most other coins, they did not know how to send it out of sequence (forwarded) timestamps in order to generate negative solvetimes. Soon after they forked, a negative solvetime came though and difficulty went to zero because the denominator was really high. A line of code attempted multiplication of a signed and unsigned integer, i.e. : double = size_t * int64_t. The high bit for sign in int64_t was treated as a really large number. This is a very basic mistake 3 of us should have caught before IPBC tripped over it and had to debug the code to identify the problem. Intense did not see this change and has to fork a 3rd time (first time they had the old Masari code). I feel responsible for half the forks and bloating people's code with multiple LWMA's. The main problem is that too many needed it too fast.
A minor but ugly bug. The timestamp and cumulative difficulty vectors in CN are sized to N before they're passed to LWMA. The fix is to set difficulty_window to N+1 in the config file, then get N inside LWMA from N=difficulty_window - 1. In some LWMA versions out there originating from the initial Masari code, the LWMA is using N=59 when it looks like N=60. There's a quiet resetting of N at the top of the LWMA code. Further below that, there's an "N+1" that would have been correct if N were correct, but since it's not, it should result in a 1/60 = 1.7% error in difficulty. But it turns out that due to integer handling, there's a round off that should have caused some error, but instead it corrects the other error if N is an odd number.
As discovered in the recent Graft fork, even with the FTL = 500 fix, big miners can still play havoc with CN coins due to a bug in CN. They can "own the MTP" which can result in blocking all other miners and pools from submitting blocks if the "Jagerman MTP Patch" is not applied ( @jagerman ). This is a not an LWMA problem but something that fixes a vulnerability in all DAs if a miner has > 50% power.
Sometimes devs want to make improvements to the LWMA. Normally they want to make it respond faster by lowering N. Graft tried an ATAN() function. All attempts so far have lowered its performance. I'll change the LWMA page if a modification shows an improvement. A Dynamic LWMA is in the works.
With the FTL limit lowered, I can remove a +7xT timestamp limit. This will allow it to drop faster after bad hash attacks without losing bad timestamp protection. I have been hesitant to remove the +7 because if a coin does not use it and does not set their FTL correctly, a catastrophic timestamp exploit is allowed even with < 30% hashpower. I could make the code do an if / then based on FTL setting to set or remove +7xT limit. I have opted to change the -7xT limit to -FTL because negative solvetimes should only occur if there was a fake forward timestamp. If there is a fake reverse timestamp, to drive difficulty up (there can be profitable reasons for this, not just malicious) then the tighter reverse limit helps.
A certain theoretical malicious attack is now stopped by using MTP=11 instead of 60.
Oscillations in LWMA start appearing. In March 2018 Niobio started LWMA and was showing an oscillation pattern. It soon subsided. Then BTC Candy switched from an SMA to LWMA and saw improvement, but it still had TERRIBLE oscillations. It was constantly on the verge of collapse small CN default coins, but somehow survived. Then Iridium started having moderate oscillation problems before it forked to a new POW. Then Masari forked to a new POW and started having moderately bad oscillations. The POW changes in Monero were appeared to be causing either Nicehash or Asics to start focusing on certain POWs which exposed LWMA's weaknesses: it needed to respond faster and not fall too far after an attack. Wownero and Intense started showing minor oscillations in May. About 15 other LWMA coins were still doing good. I tried a Dynamic LWMA and Slipstream EMA, both of which I later determined were likely to cause as many problems as they solved, so I abandoned them. Karbo, Technohacker, Niobio, and Wownero were already coding Slipstream and running testnets when I abandoned it. BTC Candy made a change about May 17 that is so far (only 6 days) working great for them. My review of their code indicates it may not help the smaller types of oscillations.
The oscillations continued on BTC Candy and Masari into June 2018, while being minor on other coins. Looking at it closely, it had the appearance of a single big miner who loves the coin, and is willing to constantly mine it at a higher difficulty than others. The truth is that the POW seemed to make it more profitable for a smaller goup like ASICs or Nicehash than GPU miners. The problem with Masari was repeatedly clear 5 to 10 times per day: big "miner" drove it up 20% to 30% in 10 to 20 blocks, then stopped. Since other miners were not present, that block took 7xT to 20xT to solve instead of 30% longer. Seriously clear: last 3 blocks took T/10 and the 4th one took 20xT. The long delay caused a 20% to 30% drop, and the miner came back, repeating the problem. Stellite did like BTC Candy and turned my "Dynamic LWMA" idea of triggering on a sequence of fast solve times into a fast rise without a symmetric fall which I was sort of opposed to on mathematical grounds. But the worst that can happen is that average solvetime will be a little too high and that will occur only if there are constant attacks. Their main net results were better than LWMA, so I experimented with many different modifications and came up with some a lot simpler than theirs and I believe better with LWMA-2.
In June 2018, four Zcash clones started looking into LWMA, so I refined BTG's code to be more easily used in those BTC-like coins. Over 50 coins have LWMA on mainnet or testnet. Several have LWMA-2 on testnet and are planning to switch to it in the next fork.
In September 2018 a > 50% selfish mine attack was performed on an LWMA that was able to lower difficulty and get 4800 blocks in 5 hours. It's the result of an error I made in handling negative solvetimes that was present most of LWMAs. The attack used a method I seem to have discovered and publicized 60 days earlier, but I did not realize the attack applied to my own algorithm. It still applies to LTC, BCH, Dash, and DGW coins, unless there is a requirement outside the DA to limit out-of-sequence timestamps more strictly than the MTP, or unless the MTP is used as the most recent block in the calculation. A different method is used in LWMA-3 and LWMA-4 so developers do not need to do work outside the algorithm, and so that there is not a delay caused by using the MTP protection like Digishield does (which adds to oscillations). LWMA-3 refers to coins that have the timestamp protection, and probably contain LWMA-2's jumps.
November 1. It looks like LWMA-2's 8% jumps (when sum last 3 blocks solvetimes < 0.8xT) may not have helped the NH-attacked coins. Lethean, wownero, graft, and saronite still look very jumpy and have ~10 or so blocks delayed > 7xT which normally almost never occur. Bitsum's LWMA-2 made things a lot worse because I did not realize until now that negative solvetimes make LWMA difficulty jump up a lot more. LWMA-4 has been modified to refine the LWMA-2 & 3 jumps to be more aggressive and yet a lot safer (not make things worse). It required a lot of work and makes the code a bit more complicated. Coins not needing it should stick with (fixed) LWMA. LWMA-4 also introduces using only the 3 most significant digits in the difficulty, forcing the rest to 0, for easier viewing of the number. Also, the lowest 3 digits will equal the average of the past 10 solvetimes, helping everyone to immediately see if there is a problem.
About January 2019: although LWMA 2, 3, and 4 seems better on most coins than LWMA-1, when there is a persistent problem like there has been on Wownero, they seem to make it worse. Also 2, 3, and 4 may bias the performance metrics to look better than they are. For these reasons I've deprecated all versions except LWMA-1.
May 16, 2019. I discovered lowering FTL to greatly reduce timestamp manipulation results in allowing a 33% Sybil attack on nodes that ruins the POW security. Many devs from many coins were involved in the FTL discussions specifically to determine if there was a reason not to lower it too much. I blame the original BTC code for not making the code follow its proof of security. If changing a constant affects the security of an unrelated section without warning, it's not good code. If your coin uses network time instead of node local time, lowering FTL < about 125% of the "revert to node time" rule (70 minutes in BCH, ZEC, & BTC) will allow a 33% Sybil attack on your nodes, So revert rule must be ~ FTL/2 instead of 70 minutes. If your coin uses network time without a revert rule (a bad design), it is subject to this attack under all conditions See: zcash/zcash#4021 for more details.
Problems I've been a part of
Other than wasting Zcash developers' time and sending Cryptonote clones down the path of Zawy v1 SMA N=17 when the default Digishield would have been better (or just lowering their N and removing the lag, which is basically what Zawy v1 was except N was too low) other problems I've been at least involved in:
Bitcoin Gold also suffered greatly from following my recommendation of converting their Zcash-derived Digishield to an SMA N=30. It may have worked fine if not substantially better than Digishield (with the default values but not an optimized Digishield), except there is a +16 / - 32% "POWLimit" in Digishield done in a way that is derived from BTC's 4x / 1/4 POW limit. I thought the POW limit was referring to a per-block allowable decrease in difficulty. The Digishield terminology implies the creators of the limit thought so too. It's checked and potentially applied to every block, and a 16% / -32% limit makes send, although I objected to it not being symmetrical. It would have been not nearly as bad if the limit were symmetrical. But I knew a 16% limit on D per block would rarely be enforced, so I acquiesced to keeping the limits in and not even bothering to make them symmetrical. Keep in mind BTG was trusting me to make the correct final decision and did exactly as I recommended. The result has been a constant but limited oscillation and a block release rate that is about 10% too fast. The 16% actually limits the per block increase to 0.5% to 1.5% exactly when it is needed the most. I had not tested it as it was coded, but tested my incorrect interpretation of it. It may have been OK, maybe better than Digishield, if the limits were symmetrical. THe limits are almost never reach in Digishield because it is too slow in responding to activate the limits, except in startup where it causes a 500 to 1000 block delay in reaching the correctly difficulty. The error is a much milder form of BCH's EDA's asymmetry mistake. They would have been fine if it were symmetrical, i.e. if the allowed increase were as fast as the decrease. Since BTG had reached $7B market cap, this was the biggest mistake in economic terms.
First error in LWMA: see item 1) in above history of LWMA. I didn't create the error, I found it pretty soon, and I got them to correct it ASAP. But I was involved. I did not actively watch to see what code they were writing. I was unable to stop other coins from copying it.
2nd and 3rd errors in LWMA: again see history above, items 2) and 3). Again, it is and is not my fault for the same reasons.
Item 4 in LWMA history was "caused" by LWMA being a lot faster. Like the BTG problem, a faster algorithm exposed an existing ... feature ... in someone else's code. It could only be exploited by a > 50% miner, so some (like a Monero commenter) would say it's not an issue we can or should worry about. However, > 50% miners are not intentionally harming coins unless they can find a way to lower difficulty while they are mining. I found the way to address this problem: simply lower the FTL. This issue also demonstrates something: > 50% "attacks" are daily life for possibly every coin that is not one of the top 20. Zcash is the 2nd largest for its POW and sees > 200% mining increases (66% miner(s)) come online to get 20 blocks at cheap difficulty at least once every day. Problems caused by > 50% miners can and should be addresses where it can. Getting back to my fault here: an unkind perspective is that LWMA caused this. I think a more accurate description is that by using the only way possible to protect small coins (making it faster) a problem was created and repaired, at a cost of making the newest adopters of LWMA fork twice. Technical detail on this problem describing why lower N exposes the problem: difficulty can be temporarily lowered to (N-FTL)/N where FTL is in terms of a multiple of the coin's T.
See item 5 in LWMA history. I didn't write the code, but I approved it, and a coin trusted my recommendation.
Item 10 in LWMA is something I was aware of from the very beginning, but did not carefully measure the extent of the problem. I thought it was a remote possibility. Again, it is only possible with a > 50% miner. Maybe I had not realized back then that > 50% mining is actually addressable.
Item 11. Four devs had started testnets on one of my ideas I had strongly promised would work, but then found out it had an exploitable hole. Several devs were good-spirited to tolerate LWMA-2 constantly being refined ... after I said it was definitely finished each time.
I recently noticed coins who need a lower D have an unexpectedly high Std Dev of their D, and vice versa. After a lot of testing and watching many live coins, it seems resilient. This can enable the algorithm to automatically adjust N to optimize performance.
This is a place holder for a possible future article on this.
this was for a scratchpad
See this page for LWMA-4
[ Edit: This article is a little dated. I now have all the equations in integer format and the solvetime limits limits should be -FTL and +6 (instead of +7 and -6) where FTL = future time limit nodes allow blocks to have and is 3xT as described on the LWMA page. Otherwise there is a timestamp exploit by > 50% miners that can greatly lower difficulty. ]
The simplest algorithm is the Simple Moving Average (SMA)::
next_D = avg(D) * T / avg(ST)
where D and ST are N of past difficulties and solvetimes. The N in the two averages cancel which can code and compute a little more efficiently as:
next_D = sum(D) * T / sum(ST)
Sum(D) is just the difference in total chain work between the first and last block in the averaging window. Sum(ST) is just the difference between the first and last timestamp. This is the same as finding your average speed by dividing the change in distance by the change in time at the end of your trip. I do not use this sum() method because it allows a bad timestamp to strongly affect the next block's difficulty in coins where future time limit is the normal 7200 seconds, and if T=120 and N=60 (in many of them).
The SMA is not very good because it is simply estimating the needed difficulty as it was N/2 blocks in the past. The others try to more accurately estimate current hash rate.
For whatever reason, using the average of the targets instead of the difficulties gives a more accurate avg solvetime when N is small. Since you have to invert the target to get the difficulty, this is the same as taking the harmonic mean of the difficulties.
# Harmonic mean aka Target SMA method
next_D = harmonic_mean(D) * T / avg(ST)
# or
next_D = max_Target/avg(Target) * T / avg(ST)
# or
next_Target = avg(Target) * avg(ST) / T
max_Target = 2^(256-x) where x is the leading zeros in the coin's max_Target parameter that allows difficulty to scale down.
The best way to handle bad timestamps without blocking reasonably-expected solvetimes requires going through a loop to find the maximum timestamp. There are other ways to deal with bad timestamps, but this is the best and safest.
# SMA difficulty algorithm (not a good method)
# This is for historical purposes. There is no reason to use it.
# height-1 = index value of the most recently solved block
# Set param constants:
T=<target solvetime>
# For choosing N and adjust, do not write these equations as code. Calculate N and adjust,
# round to integers, and leave the equation as a comment.
# N=int(40*(600/T)^0.3)
# adjust = 1/ (0.9966+.705/N) # keeps solvetimes accurate for 10<N<150
for (i=height-N; i<height; $i++) {
avgD += D[i]/N;
solvetime = timestamp[i] - timestamp[i-1]
avgST +=solvetime/N
}
next_D = avgD * T / avgST * adjust
# I've used avgD and avgST for math clarity instead of letting N's cancel with sumD/sumST
# H-SMA or Target-SMA difficulty algorithm
# Harmonic mean of difficulties divided by average solvetimes
T=<target solvetime>
# Calculate N round to an integer, and leave the equation as a comment.
N=int(40*(600/T)^0.3)
# height-1 = index value of the most recently solved block
for (i=height-N; i<height; $i++) {
sum_inverse_D += 1/D[i];
# alternate: avgTarget += Target[i]/N;
solvetime = timestamp[i] - timestamp[i-1]
# Because of the following bad timestamp handling method, do NOT block out-of-sequences
# timestamps. That is, you MUST allow negative solvetimes.
if (solvetime > 7*T) {solvetime = 7*T; }
if (solvetime < -6*T) {solvetime = -6*T; }
avgST +=solvetime/N
}
harmonic_mean_D = N / sum_inverse_D
next_D = harmonic_mean_D * T / avgST * adjust
# alternate: next_Target = (avgTarget * avgST) / (N*N*T) # overflow problem?
Digishield v3 has a tempered-SMA that works a lot better than simple SMA algos .... provided the 2 mistakes in Digishield v3 are removed (remove the 6 block MTP delay and the 16/32 limits). The tempering enables fast response to hashrate increases while having good stability (smoothness). Its drawback compared to the others is 2x more delays after hash attacks. Even so, it's response speed plus stability can't be beat by LWMA and EMA unless they use its trick of tempering. It cost them some in delays, but they still have fewer delays than Digishield. The root problem is that although Digishield uses a small N to see more recent blocks than an SMA, it's still not optimally trying to estimate current hashrate like LWMA and EMA. PID and dynamic versions of LWMA and EMA can also beat Digishield without copying it. But Digishield is not far behind anyone of them if stability is more important to you than delays.
# Zawy modifed Digishield v3's (tempered SMA)
# [edit this is very dated. New versions revert to the target method and does better timestamp limits. ]
# 0.2523 factor replaces 0.25 factor to correct a 0.4% solvetime error. Half of this
# error results only because I used a difficulty instead of target calculation which
# makes it an average D instead of the more accurate average target (which is harmonic mean of D.)
# This algo, removes POW limits, removes MTP, and employs bad timestamp protection
# Since MTP was removed. Height-1 = index value of the most recently solved block
T=<target solvetime>
# Recommended N for balance between the trade off between fast response and stability
# If T changes away from Zcash's T=150, the stability in real time will be the same.
# N=17 for T=150, N=11 for T=600
N=int(17*(150/T)^0.3)
for (i=height-N; i<height; $i++) {
sumD += D[i];
solvetime = timestamp[i] - timestamp[i-1]
if (solvetime > 7*T) {solvetime = 7*T; }
if (solvetime < -6*T) {solvetime = -6*T; }
sumST +=solvetime
}
sumST = 0.75*N*T + 0.2523*sumST # "Tempering" the SMA
next_D = sumD * T / sumST
I've tried modifying the tempering and I can't make it better. I've tried using the tempering in non-SMA algos but there was no benefit. I tried using harmonic mean of difficulties, but it did not help.
Re-arranging Digishield's math gives:
next_D = avg(17 D) * 4 / ( 3 + avg(17 ST)/T)
The EMA can be expressed in something that looks suspiciously similar. The exact EMA uses an e^x. But e^x for small x is very close to 1+x. This is actually a vanilla EMA that's not as exact. It parallels Digishield (but is substantially better:
next_D = prev_D * 36 / ( 35 + prev_ST/T)
The following are articles I plan to write (largely re-writing things that are already somewhere on GitHub.
Begin update: This article is long and complicated because I wanted to cover every possibility, such as RTT which I'm sure no one is going to push. To make this long story short, this is all I think a dev needs to know to implement it.
next_target = previous_target * (1 + st/600/N - 1/N )
st= previous solvetime
Clipping: An attacker with say 10% hashrate could set large forward times to lower difficulty to where he could get a lot of blocks and then submit them when that time arrives. He can't win a chain work race, but Mark L in a comment below was concerned this could enable spam if there is no clipping. Clipping could be done with max solvetime allowed like 7xT. This is the same as a max drop in difficulty. It should be a bit more than you normally expect to see if HR is constant. It can reduce the motivation for constant on-off attacks at a cost in slightly more delays depending on the size of HR changes but I was not been able to see a clear benefit from 6xT clipping after recommending it to a lot of alt coins. I recommended it because LWMA has a bigger problem of dropping too much when on-off mining leaves. There should not be any clipping on how much difficulty rises unless it is many multiples of the max drop. Otherwise a timespan limit attack is possible. To give an example of how clipping makes it harder to spam, a 10% HR miner could send a timestamp 333xT into the future and immediately drop an N=72 EMA to 1% of it's former difficulty. It would take 55 blocks if clipping is limited to 7xT and have a net cost of 12.4 blocks at the initial difficulty instead of just 1 block. So clipping in this example makes a spam attack 12x harder.
End update
A good difficulty algorithm can allow more time to consider a POW change. If BCH switches DAs, the best options seems to be the EMA (@dgenr8's improvement to @jacob-eliosoff's) such as the one @Mengerian is doing with bit-shifting is pretty much the same as @markblundeberg's re-invention of the perfect algorithm that Jacob once briefly considered (but not in the Real Time Target (RTT) form).
The following are all the things I know of that need to be considered in implementing an EMA.
The following are testing results on the various options. The attack models BCH's current situation which is a fairly rigorous test compared to other possible settings. Other settings result in similar relative results. The target solvetimes were tweaked to give the same avg solvetime so to prevent an unfair advantage. All the algos except the RTT have an N setting that gives the same Std Dev in difficulty as SMA N=144 under constant hashrate.
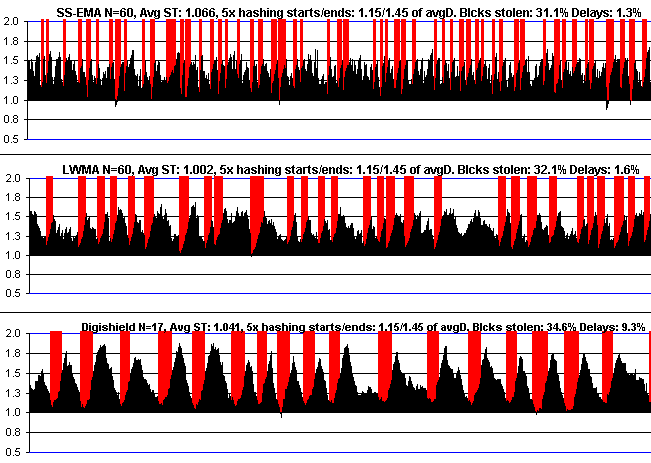
The best way to a judge a good algorithm from these charts is to see if the blue lines (avg of 11 solvetimes) are not going up and down too much, and also for thin green bars which is how many blocks (not time) the attacker is getting before difficulty has risen above his "stop mining" point. The stolen metric is the time-weighted target the attacker faced verses the average. If it's 3% then his target was 3% higher than a dedicated miner (his difficulty was 3% lower). The delay metric is the sum of solvetimes in terms of target solvetimes that took 6xT, minus 2xT, expressed as a percentage of the total number of blocks.
SMA_ Target ST/avgST= 599/600.357 N= 144
attack_size: 600 start/start: 130/135, StdDev STs: 1.283
delays: 9.6% stolen: 5.4%

EMA with 2-block delay on timestamps
Target ST/avgST= 594/599.769 N= 80
attack_size: 600 start/start: 130/135, StdDev STs: 1.270
delays: 6.3% stolen: 4.4%

EMA (normal)
Target ST/avgST= 594/599.721 N= 80
attack_size: 600 start/start: 130/135, StdDev STs: 1.265
delays: 5.5% stolen: 3.3%

Marks RTT "EMA"
This is identical in results to a normal EMA using current block's solvetime instead of previous block's.
Target ST/avgST= 602/600.094 N= 80
attack_size: 600 start/start: 130/135, StdDev STs: 1.130
delays: 1.4% stolen: 0.7%

LWMA (looks same as normal EMA)
Target ST/avgST= 598/600.321 N= 144
attack_size: 600 start/start: 130/135, StdDev STs: 1.270
delays: 5.7% stolen: 3.4%

TSA (A slow normal EMA N=80 with a fast EMA N=11 RTT riding on top)
The negative stolen metric indicates it's costly to try to pick a low difficulty to being mining with a high hashrate. The blue + symbols are the target the miner actually had to solve. The purple solid line is the difficulty that goes on the chain. If you look closely, almost no + marks in the green areas (attacks) are below the average difficulty. This is because the big hashrate is doing a fast solve which causes difficulty to be higher. Notice the delays and blue line swings are not any better, but in practice they will a lot better because big miners will be much less likely to participate if a 2% loss like this is the outcome as opposed to the current 5.4% gain in SMA. I discuss this more in my TSA article.
Target ST/avgST= 595/599.93 N= 80 and M=11
attack_size: 600 start/start: 130/135
StdDev STs: 1.13
delays: 2.13% stolen: -1.23%

This shows the difference between an EMA with a 2-block solvetime delay (like the chart above) WITH a 1 block delay in targets. It's a disaster.
[update: the e^x forms I described in this issue in 2018 are unnecessarily complicated and they give almost identical results to ASERT. The simpler way to view this content is that the primary equation presented:
next_target = prior_target * (1+t/T/N-1/N)
is just an EMA where t=solvetime of previous block, T = desired block time, N is a "filter", and t/T is the estimate of how much previous target needed to be adjusted. To show this is just an EMA, Wikipedia's EMA: is:
S[i] = A*Y[i] + (1-A)*S[i-1]
Our estimated next difficulty based on previous solvetime and previous difficulty is
Y[i] = S[i-1]*adjustment_needed
which gives:
target[i] = A*target[i-1]*t/T + (1-A)*target[i-1]
Using, A = α = 1/N, this simplifies to the 1st Target equation above.
We should have guessed (and JE did) this could be improved with replacing the implied 1+x in the 1st equation with e^x to get the later-discovered-as-possibly-ideal ASERT. Wikipedia says EMA is a discrete approximation to the exponential function. So this leads us to relative ASERT:
next_target = prior_target * e^(t/T/N-1/N)
In an upcoming issue (it is now January 2022 in case I do not come back to link to it) I'll argue adjustment_needed should not be t/T but be
adjustment_needed = 1+ error =1 + e^(-median_solvetime/T) - e^(-t/T) = 1.5 - e^(-t/T)
In words, this adjusts based on the probabilities of the solvetimes we expect. It is the ratio of the observed to the expected solvetime probability for individual solvetimes. We expect to see a median solvetime which for an exponential distribution is e^(-t/T) * T= 0.5*T, not the long term average. A simple t/T does not take into account probabilities of the t's we expect. So the proper EMA from this assumption is
target[i] = A*target[i-1]*(1.5 - e^(-t/T) ) + (1-A)*target[i-1]
which is
next_target = previous_target * (1 + 0.5/N - e^(-t/T)/N )
and if we guess this should be in an ASERT-like form we can guess this is
next_target = previous_target * e^(0.5/N - e^(-t/T))
This is just replacing the error signal "t/T -1" in ASERT with 0.5-e^(-t/T). This works lot a better than ASERT in the sense of getting the same stability as ASERT with 1/3 the value of N. It results in 1/2 as many "blocks stolen" compared to dedicated miners during on-off mining at a cost of very slightly longer delays and avg solvetime being longer during the attack.
end update
Summary: This explores the theoretical origins of EMA algorithms. The only sensible one to use that does not have problem due to integer math, negative difficulties or zero solvetimes is:
simplified EMA-TH (floating point for clarity)
next_target = previous_target * (1+t/T/N-1/N)
next_difficulty = previous_difficulty / (1+t/T/N-1/N)
ETH does something like the above WITH the integer round off error and surprisingly does OK.
simplified EMA-TH (actual code for integer math with less chance of overflow problem in target)
k=10000;
next_target =(previous_target/ (k*N)) * (k*N+(k*t)/T-k)
next_difficulty =( previous_difficulty *k* N )/(k*N+(k*t)/T-k)
Bit shifting can be used to replace the above division.
Notation:
There are two different ideal forms of the EMA shown below that are equal within 0.02% for most solvetimes, and equal to within 0.005% on average. The differences between them all can be attributed to
e^x =~ 1+x for small x which results in the simple forms
1+x =~ 1/(1-x) when x is small which is the distinction between JE and TH.
JE and TH refer to Jacob Eliosoff's original version, and TH refers to a precise form of Tom Harding's simple version . The simplified JE-ema can result in divide by zero or negatives for smallish N, or if a big miner keep sending "+1" second timestamps that ends with an honest timestamp that throws it negative. The more precise e^x and "accurate" JE-ema versions do not have this problem and are slightly better than TH versions at small N. But it is very difficult to get the e^x versions to not have error that cancels the benefits when working in integer math. The e^x needs to accurately handle values like e^(t/T/N) which for t=1, T=600, and N=100 is e^(0.000017). Even after using e^(1E6*t/T/N) methodology the avg solvetime the error from floating point that I could not resolve was 1% plus there was another 1% error at N=100 from being able to let t=0 in these versions due to divide by zero.
ema-JE = prev_target / ( T/t+(1-T/t)*e^(-t/T/N) )
ema-TH = prev_target * ( T/t+(1-T/t)*e^(+t/T/N) )
The bottom of this article shows how this comes from common EMA terminology about stock prices. After Jacob Eliosoff derived or maybe guessed this from experience with EMAs and some thought, I later found out his result has applications in measuring computer performance
A e^x = 1+x+x^2 substitution can be used that gets rid of the e^x version, but it introduces a much greater potential for overflow. It
k=t/T/N
accurate ema-JE = prev_target / (1+1/N+k*(k/2-1-1/2/N)) // ** The most accurate one **
// To do the above in integer math, the follow can be used but has large overflow potential:
accurate ema-JE = (prev_target * (N*T*N*T*2)) / (2*T*N*T*N+2*T*T*N+ST*(ST-2*T*N-T))
// But a difficulty version does is not a problem i D is large:
accurate ema-JE = (prev_target + prevD/N + (prevD*ST*ST)/(N*T*N*T*2) - prevD*ST/T/N -(prevD*ST)/(N*N*T*2)
accurate ema-TH = prev_target * (1-1/N+k*(k/2+1-1/2/N))
With the simpler substitution e^x = 1+x, another near-perfect algorithm is possible, as long as N is not smaller than about < 20. These can have zero and divide by zero problems
simplified ema-JE = prev_target * N / (N-t/T+1) // Do not use this one.
simplified ema-TH = prev_target * (N+t/T-1) / N // This is the most sensible one. Simpler small error.
(just inverse for difficulty versions)
Problems
As PID Controller
The EMA might be viewable as a PID controller that takes the Poisson distribution of the solvetimes into account. A PID controller is a*P+b*I+c*D where P is present value, I is the integral (sum) of previous values, and D is the derivative (slope) of recent values. So a PID controller is taking present, past, and an estimate of the future into account. To see it possibly here, the ema-JE can be written in the form:
next_difficulty = prev_D*T/t*(1-e^(-t/T/N) + t/T*e^(-t/T/N) )
1-e^(-t/T) is the single-tail probability of a solvetime being less than t.
t/T*e^(-t/T) is the probability density function of solvetimes. It is also the derivative of the former.
The next_D (aka 1/(target hash)) keeps a running record of previous results, so in a sense it's like a summation. The summation can be seen if you recursively substitute prev_D with the equation that came before it, and expand terms. I can't see how that would lead to the PID equation, but I wanted to point out the 3 elements of a PID controller seem to be present. A similar statement can be made about the WHM. The SMA and Digishield seems to be like a PI controller since it does not take the slope into account.
The EMA can be the starting point of a fully functional PID Controller that does not work noticeably better than the above. This is because PID controllers are needed in systems that have any kind "mass" with "inertia" (which might be an economy or public opinion, not merely restricted to the physics of mass). The "inertia" leads to 2nd order differential equations that can be dealt with by PID controllers. Difficulty that needs to have faster adjustment as might be needed by a PID controller does not have any inertia. Long-term dedicated miners have inertia, but the price/difficulty motivation of big miners jumping on and off a coin (the source of a need for a controller) is a non-linear equation that invalidates the relevance of PID controllers.
I've been promoting this algorithm, but after further study, the
LWMA and Simple EMA are the best
Links to background information:
Original announcement of the algorithm
Handling bad timestamps
Determining optimal value of N
Other difficulty algorithms
All my previous inferior attempts
Note: there is a 2.3 factor to make the N of this algorithm match the speed of the WHM.
# EMA-Z Difficulty Algorithm
# credits: Jacob Eliosoff, Tom Harding (Degenr8), Neil (kyuupichan), Scott Roberts (Zawy)
# Extensive research is behind this:
# Difficulty articles: https://github.com/zawy12/difficulty-algorithms/issues
# https://github.com/kyuupichan/difficulty
# https://github.com/seredat/karbowanec/commit/231db5270acb2e673a641a1800be910ce345668a
# ST = solvetime, T=target solvetime, TT=adjusted target solvetime
# height - 1 = most recently solved block.
# basic equation: next_target=prev_target*(N+ST/T-1)/N
# Do not use MTP as the most recent block because shown method is a lot better.
# But if you do not MTP, you MUST allow negative solvetimes or an exploit is possible.
# Ideal N appears to be N= 20 to 43 for T=600 to 60 by the following formula.
# ( Note: N=20 here is like N=46 in an SMA, WHM, and the EMA-D )
# The following allows the N here to match all other articles that mention "N"
# An EMA with this N will match the WHM in response speed of the same N
N = int(45*(600/T)^0.3)
# But I need to convert that N for use in the algorithm.
# M is the "mean life" or "1/(extinction coefficient)" used in e^(-t/M) equations.
M = int(N/2.3+0.5)
# WARNING: Do not use "if ST<1 then ST=1" or a 20% hashrate miner can
# cut your difficulty in half. See timestamp article link above.
ST = states[-1].timestamp - states[-2].timestamp;
prev_target = bits_to_target(states[-1].bits);
k = (1000*ST)/(T*M);
// integer math to prevent round off error
next_target = (1000*prev_target * (1000-1000/M+(k*k)/2000+k-k/(2*M) )/1000)/1000;
These are my comments each section of Orbital coin's difficulty algorithm. I've simplified the code for readability. There's no missing code.
// POW only
// ####### Begin OSS algorithm #########
nTargetSpacing = 360;
nTargetTimespan = nTargetSpacing * 20
nActualTimespanShort = timestamps[-1] - timestamps[-5];
nActualTimespanLong = timestamps[-1] - timestamps[-20];
/* Time warp protection */
nActualTimespanShort = max(nActualTimespanShort, (nTargetSpacing * 5 / 2));
nActualTimespanShort = min(nActualTimespanShort, (nTargetSpacing * 5 * 2));
nActualTimespanLong = max(nActualTimespanLong, (nTargetSpacing * 20 / 2));
nActualTimespanLong = min(nActualTimespanLong, (nTargetSpacing * 20 * 2));
The above prevents it from changing very much if the last 5 or 20 blocks were 2x too fast, or 2x too slow. For N=5 or 20, this is not good. nActualTimespan limits should be to prevent big problems, but with N=5 and 20, it gets activated a low. It limits how fast the algorithm can change, especially during a hash attack. BCH uses the same 2x factor, but they have N=144 and more importantly they are a large coin with stable hash rate. So it will not get activated unless there is a catastrophic change. BTC uses 4x as protection for catastrophic situations, again with a much larger N=2016.
/* The average of both windows */
nActualTimespanAvg = (nActualTimespanShort * (20 / 5) +
nActualTimespanLong) / 2;
This above gives equal weighting to the short and long windows. This is good It's like a really mild form of LWMA. I show at the bottom that it's good, so this idea could be used in Digishield coins to improve them.
/* 0.25 damping */
nActualTimespan = nActualTimespanAvg + 3 * nTargetTimespan;
nActualTimespan /= 4;
This is Digishield's 75% dampening, not 25%. It is saying "we believe the previous difficulty was 75% correct and we'll give the recent timestamps 25% vote on what the next difficulty should be. It's better than simple moving averages, but not as good as EMA and LWMA.
/* Oscillation limiters */
/* +5% to -10% */
nActualTimespanMin = nTargetTimespan * 100 / 105;
nActualTimespanMax = nTargetTimespan * 110 / 100;
if(nActualTimespan < nActualTimespanMin) nActualTimespan = nActualTimespanMin;
if(nActualTimespan > nActualTimespanMax) nActualTimespan = nActualTimespanMax;
Since the above comes after the 75% Digishield dampening, it's like limits that are 4x these limits when expressed in terms of the previous 2x limits. That is, they are basically +20% and -50% limits, so it is overriding most effects the 2x limits had. I confirmed this by testing. This is not how you want to limit difficulty changes. There should not be any limits except for extreme circumstances, otherwise you could have used a larger N to get the same benefits with fewer problems. The +5% limit would have enforced a 0.2% rise per block during hash attack attacks, if the big error in the last line of this code were not in place. That error prevents this error from causing a problem. Start up is like a hash attack and it takes Digishield 500 blocks to reach the correct difficulty with a 16% limit where this one has 5%, so if it were not for the last line of code, it would have taken Orbitcoin 1500 blocks. See this for a detailed review of the problem.
Making it asymmetrical with +5% and -10% instead of +10% / -10% causes two other problems. The first is that avg solvetime will be a little faster than target. The bigger problem is that it invites oscillations. It's slow to rise, so big miners stay on longer. It ends up with a longer delay which allows it to drop faster, especially since the larger limit is allowing it to drop faster. The extreme case was the fantastic failure of BCH's initial asymmetrical EDA. A milder case is what I allowed to happen to BTG by not removing the +16% and -32% limits from the Digishield code when i made it faster. These limits made it slower and with bad oscillations.
However these problems I normally expect from +5% and -10% limits did not occur in Orbitcoin because the of the next error. The combined errors gives significantly better results than either error alone, but still terrible results.
/* Retarget */
bnNew.SetCompact(pindexPrev->nBits);
bnNew = bnNew * nActualTimespan / nTargetTimespan;
// ######## End OSS algorithm ###########
The above uses the previous target instead of doing like Digishield and using the avg of the previous difficulties. My testing indicates using the average of the past 20 instead of 1 or 5 is a LOT better. EMA is able to do this, but it's done in a very specific way.
The following code is what Digishield does, expressed to look like the OSS above. It's a lot simpler and gives a lot better results. I didn't include Digishield's limit because they are never activated except at start up where it causes a 500 block delay in coins reaching the correct difficulty. I've also removed the 6-block MTP delay.
nActualTimespan = timestamps[-1] - timestamps[-17];
nActualTimespan = ( nActualTimespan + 3*nTargetTimespan) / 4;
bnNew = Average_17_bnNew * nActualTimespan / nTargetTimespan;
The following compares OSS and this simplified version of Digishield/Zcash. Reminder: Digishield/Zcash is not as good as the Simple EMa and LWMA, especially with the MTP 6 that it normally has.
Constant hash rate OSS verses Digishield


Typical Hash attack OSS verses Digishield
Digishield scores a lot better because it does not accidentally go low as often (which invites a hash attack) These are hash attacks based on simulation of miner motivation: they begin if D drops 15% below average, and end when it is 20% above average. These results are robust for a wide range of start and stop points.


OSS worse WITHOUT the +5%/-10% limits
This shows the results of OSS are worse if the 5%/-10% were not in place.

Digishield worse WITH the +5% / -10% limits

Digishield worse when using previous bnNew instead of avg

Using OSS idea to improve Digishield
The following is a modified Digshield using the 5/20 idea from OSS. I used 5/17. It is pretty much the same as Digishield, except with 1/2 the delays. If I lower the 17 to 14, it is very competitive to LWMA. It has fewer delays with slightly more blocks stolen, at the same speed of response and stability.

Unified Equation for Difficulty Algorithms
next_D = avg(n Ds) *r / ( (r-1) + sum(n w*STs)/sum(n w's)/T )
r=1, w=1 is SMA
n=1, w=1 is EMA
w=1 is Digishield-type
r=1 is LWMA
all 3 variables are used OSS
w here is a weighting based on the n. Notice it's 1 for all but LWMA, which is a simple linear weighting, giving the more recent n's more weight. It can be added to code simply, but other weightings can't. Actually, this is an inferior form of the equation. It needs to be based on Targets.
next_T = [(r-1) + sum(n w*STs)/sum(n w's)/T] / (avg(n Ds) *r)
Please do not use MTP as the most recent block or use any other filters or limits.
MTP is the 2nd worst way to deal with bad timestamps.
If you are going to block out-of-sequence timestamps or disallow negative solvetimes,
then read my "Handling Bad Timestamps" article to make the modification,
otherwise you are potentially opening the coin to a catastrophic exploit. Do NOT
simply say if solvetime < 1 then solvetime = 1 unless you have the other required code.
Hi,
Is there a way to implement it on BitcoinZ coin ?
Knowing that it is based on Zcash.
Thank you
I thought I was completely finished studying difficulty, but important things keep coming up. The previous interesting question I didn't expect was how to do a difficulty algorithm for DAGs. I always thought there wasn't much one could do in difficulty and it was just a game (puzzle) to find the perfect one. I expected it to be only marginally better than simple moving average, and that's totally true for large coins, as BCH's new algo has shown. But I was totally wrong as far as it only being a mostly-pointless game. It's turned out that a good knowledge has been crucial in solving important problems i DAGs and VDFs (which are the future), not to mention quickly seeing when teams much smarter than me (like Chia & Ethereum) mess something up. Or seeing when an important figure like "MF" has a scheme that appears super-intelligent and yet is really awful once the wool is pulled back, making me think certain BIPs in BTC need to be rejected until a different big name is behind it. I mean we mortals have to depend on the anti-scientific appeal to authority, aka the centralization of dev reputation, unless and until crypto is greatly simplified.
Masari deployed my modification of Tom Harding's difficulty algorithm on December 3, 2017 and it's a resounding success (so far). I follow 7 coins' difficulty performance closely, and it's the best. For the best algorithms see here.
The charts below show Masari under the 3 difficulty algorithms it has experienced, and you can see how much it has improved. The 2nd and 3rd chart are only 3 days apart, so it's an "OMG" improvement. I should mention I am largely responsible for the middle algorithm that was so bad. Here is the full chart history of that algorithm.
Although the modified SMA (simple moving average) with N=17 looks worse than the Monero N=720 before it, the delay and "hash attack" metrics are equally bad. With Monero, blocks came 20% too fast (the 0.80 factor shown for solvetime), verses 36% too slow for the N=17. Less than target solvetime indicates the Monero algorithm has an asymmetry where the difficulty is able to drop faster than it can rise. This usually results from good intentions ("We don't want delays!") gone bad ("Let's modify the SMA.")
For a better chart with Masari's full history, see here
Sumokoin's modified SMA N=17 (with a 6-block delay) performed much worse for Masari than for Sumokoin, maybe because target solvetime for Masari was 1/2 that of Sumokoin (which means N should have been larger). Karbowanek has a simple N=17 SMA without a 6-block delay, and has 1/2 the "blocks stolen" of Sumokoin probably due not having the delay. Sumokoin's modified SMA is
next_D=avg(D) * T / [0.80*avgST + 0.30 median(ST)
where ST=solvetime and T=target ST, and a 6-block delay in accepting D and ST values in order to prevent out-of-sequence timestamps (a bad idea). Masari says it appears miners were taking advantage of the median adjustment, and obviously a 6 block delay means 6 "free" blocks to big miners before the algo even starts responding.
I should mention the 3 coins here using N=17 is my fault. N=30 if not N=60 would have been a lot better for all of them. But from this past mistake, I have a better estimate on how to select N.
These show typical hashrate jumps when difficulty accidentally falls about 20% low. The magenta spikes are when the avg of 11 solvetimes were > 2.1x faster than the target, indicating a large increase in hashrate that is not a statistical accident. They are scaled down to 1/4 the 1/(avg 11 solvetime) for plotting. A peak reaching 1 is 4x the baseline hashrate. The blue or orange spikes are when avg of 11 solvetimes are >2x target solvetimes, represented unusual delays, also scaled down by 1/4th.
The first one is a Monero clone, Alloy, that suffered a 3-day delay between blocks as a result of the default Cryptonote difficulty algorithm being too slow with N=720 in a simple moving average. Below shows attack that had 4x4=16x their baseline hashrate, resulting in the average of 11 solvetimes going up to 17x4=68x longer than their target solvetime. The attackers got 250 blocks before the difficulty started rising.
Alloy switched to LWMA with N=60 and 25x attacks resulted in 2x4=8x delays. The attackers got only 30 blocks before the difficulty doubled. This occured right after the fork to the new algorithm, so the attackers were trying their old tricks, which won't work anymore. They have not come back.
[update: I later found out some of these swings in alloy were due to it having a lag in its calculations, so a normal LWMA would have reacted about 15 blocks faster. ]
The same thing occurred when Masari switched to LWMA: right after the fork, they tried to attack but didn't get many blocks, so they haven't returned in 6 months.
Here's a zoom-in view of the initial Masari attack.
This is an example of Sumokoin's problems as a result of "fixing" their Cryptonote N=720 problem with my N=17 SMA. Their coin isn't "breaking" anymore (delays are tolerable), but otherwise it's not performing very well because it accidentally varies too much from the low N averaging window. So miners are constantly jumping on and off to get cheap coins.
Karbowanec did the same thing as Sumokoin (switched from N=720 to N=17 SMA). This shows similar "constant" attacks with N=17. In both cases, it's not constantly like this. These are just good examples of when the attacks were strong.
The following shows Zcash's version of Digishield doing good. By "good" I mean you can still see the attacks, but they don't last long due to the difficulty rising. It still attracts hash attacks every time it drops a little low from accidental variation. I'm including this one just to show even on good days with a large coin the big miners are still looking for opportunities to jump on. It's N=17 algo is like an SMA with N=4x17=68 because of they way Digishield "tempers" the N=17 SMA. It also has an unfortunate delay of 6 blocks in responding due to using the MTP as most recent bock timestamp, which is just a gift to the attackers at the expense of dedicated miners. (delays are not shown)
Hush is a clone of Zcash with the same algo. It's 100x smaller in hashrate than Zcash, so it sees more problems from big Zcash miners coming by for a "friendly visit".
Bitcoin cash had some problems for the first two or three days after forking to their new DAA which is an SMA with N=144. The slow N=144 let the price get out of sync with the difficulty. The (Price+Fees)/Difficulty ratio got larger which attracted more hash power. On the left half of this chart you can see that every time the red normalized price fell below the magenta normalized difficulty (the P/D ratio got lower), they would stop mining which can be seen as solvetimes going up. And vice versa when the price went above the difficulty line: solvetimes went down which shows increased hash rate. When difficulty goes up, solvetimes will be slower even if hashrate does not change, but that is a smallish effect. Notice these solvetimes go from 0.5x to 3x the target solvetime. This means hashrate went up 3x from the avg, and 6x from the low. This is an excellent chart because it shows hashrate went 3x up and down on this big coin by mere 25% changes in the P/D ratio. N=144 on a T=600 second coin (the averaging window is 1 day) like this is too slow at times for even a big coin. Small coins with Cryptonote's N=720 and T=120 solvetime is also a 1-day window and they can't usually survive. 1-day averaging allows price to change faster than difficulty.

"A Compleat Collectioin of Englifh Proverbs" - Rev. John Ray, 1668, page 33
The following are clock and timestamp requirements for distributed consensus. Following these rules prevent all known attacks on Nakamoto consensus except a basic >50% hashrate attack. It prevents timewarp, selfish mining, and peer time attacks as well as a slew of other attacks seen in alt coins. The rules are usually broken by good intentions that add code.
Timestamp attacks result from "good intentions" or other mistakes that modify the local clock or timestamp constraints required by Nakamoto consensus security proofs. All distributed consensus mechanisms require the clock (local time) to be more secure than the consensus mechanism [1][3] and messages (blocks) must have sequential (monotonic) timestamps.[2] Allowing non-sequential timestamps in bitcoin has caused many problems. The block height is not sufficient (or necessary) because timestamps estimate hashrate to set difficulty which determines which tip has consensus, overriding block height. Timestamps estimate total hashes which are the events for Lamport ordering. A 3rd fundamental requirement of all distributed consensus mechanisms ("all" includes Nakamoto consensus because the 1978 derivation by Lamport didn't depend on the algorithm) is there must be a limit on how far in the future (ahead of local time) timestamps can be. In practical terms, to prevent all the attacks and problems described on this page, Nakamoto consensus must:
If any of the above requirements are not in place, there's an exploit.
The following are examples of bad ideas that harm the consensus mechanism. Patches on top of patches are often applied. The problems are not solved unless the patches are algorithmically at least as restrictive as the above requirements.
Most coins have # 2 which allows an attacker to get > 5000 blocks in a few hours with my timespan limit attack (if they also do not force sequential timestamps).
The following repeats the requirements above differently. The theoretical reasons are explained in the introduction further below and in the footnotes.
Short Summaries of Attacks covered:
Attacks Without a Specific Section below.
All timestamp attacks result from violating the Byzantine fault tolerance foundations, undermining the Nakamoto consensus security.
If every node points to a certain BTC chain as the correct chain and it has a massive amount of chain work, your node can unilaterally reject it if a single block is beyond your local time plus the FTL. Nakamoto consensus requires node operators to have an independent ("maximally decentralized") opinion of current time. Median of peer time in Nakamoto consensus is subject to a Sybil attack.
If we do not want a "somewhat arbitrary" but agreed-upon ordering[2], there is no consensus mechanism that does not require a "prior" consensus on time[1][3] (or a time oracle) within clock error and network delays (FLP impossibility). In Nakamoto consensus, time does not merely dictate the start and end of voting rounds (to measure votes cast or allow lottery tickets to be redeemed) as in other consensus mechanisms, it measures the number of lottery tickets purchased (hashes) in order to find the least-partitioned chain (highest number of tickets purchased aka most-work) by increasing difficulty by seeing too-fast solvetimes. We can't use any consensus mechanism to determine time without weakening the decentralization of Nakamoto consensus. So how do we get get time? Ideally, nodes determine it without reference to an authority other than their operator. The node must be its own oracle. NTP and GPS are feasible, but they are central sources that may be attacked. Even the U.S. government does not trust that GPS can't be brought down. The deepest consensus principles require nodes to unilaterally and incontrovertibly decide the time. Do not change or limit what it says beyond what the consensus security dictates (see next paragraph). Ultimately the node's oracle should be the stars, subject to any changes the UN's UTI agency makes in defining UTC. But even that's centralization. Ideally, all the nodes should operate a telescope and calibrate sufficiently frequently based on the position of the stars and the node's geographical location so that the UTI can't change the definition of UTC. BTW, other astronomical observations may enable a permissionless (maximally decentralized) source of randomness to replace the permissioned aspect of "decentralized" random beacons.
Anything that changes or restricts the oracle's (the node's) opinion of time (including the allowable timestamps range or how they are used) affects the correct estimation of hashrate aka our consensus votes (lottery ticket purchases). Any incorrect estimation of current hashrate causes harm to Nakamoto consensus. FTL, MTP, and median of peer time are all "well-intentioned" patches to our lack of a common time oracle (excepting the stars) but they all cause problems in proportion to how far they are from true time. There's a long history of reducing their values to stop future attacks. FTL is the only one that arguably should not be zero due to honest clock error. It is not unreasonable to have FTL=10 seconds. If the mining network has nodes with clock error > FTL, it can block valid winners for a time, increasing the orphan rate. The fraction of FTL to the difficulty averaging window is the fraction that manipulation can decrease difficulty in one or more subsequent blocks.
Sequential logical stamps are a requirement of distributed ordering.[2] To prevent "somewhat arbitrary" ordering, physical clocks must be used and they allow or assign any timestamp before any prior timestamp that the node approved) It appears using MTP=1 instead of MTP=11 (which means the 6th block in the past will be the "MTP block" if the 11 timestamps are in order) will force the next timestamp to be greater than previous timestamp. If all the code elsewhere is written correctly, nothing will be broken by this change and the remaining exploits in bitcoin will be impossible. Digishield and other difficulty algorithms prevent an attack from non-sequential timestamps by using the MTP block as the most recent block and this causes persistent but small oscillations. If monotonic timestamps are not used, the next best solution is to use code in the difficulty algorithm to create a "fake" sequence of monotonic timestamps when they get out of order, but not "if solvetime < 0 then solvetime = 0".
Giving miners more room to set timestamps (within the 2-hour FTL and MTP=11) appears to be from a mistaken belief that the average honest miner is setting the time. But nodes individually and unilaterally set the limit on how much time can be forwarded and miner greed of wanting blocks as minimal difficulty prevents them from holding time back.
I want reiterate that [1] shows ordering is possible without a clock. This is potentially very useful in new coin ideas. In another scheme, the time oracle can be reduced to assuming a maximum drift rate in the nodes' clocks.[4] This provides every node with the ability to survive any attack on network time, like a node looking at the stars to unilaterally determine time. In either method, they can know they have the correct system-wide consensus even if every other node in the system disagrees with them.
Definitions:
difficulty ~ 1 / target
T = target solvetime
TS = timestamp
N = blocks in a difficulty averaging window
MTP = Median Time Past = either the distance in blocks to the MTP block in the
past or timestamp of that block (typically the 6th block in past +1 second for
coins keeping the BTC MTP of past 11 blocks rule).
FTL = Future Time Limit, the largest time ahead of node time that's allowed
Note on the Verge Attack
The Verge attack seemed to have been a combination of a too-long FTL value (forward timestamps), a 1/3 and 3x timespanLimit attack, making the longest chain the one with the most blocks instead of chain work, and the attacker having a lot of hashrate in one of the algos.
I originally mistakenly called this the powLimit attack.
I discovered this while writing this article to explain the Zeitgeist attack. My own LWMA difficulty algorithm was the first to be attacked using it (that I am aware of) about 40 days after I wrote this article. I mistakenly thought mine was immune. In April 2018 LWMA coins attacked were Niobio, Intense, Karbo, Sumo, and a couple of others. I don't know if the Verge attack that occurred then used this. Typically in an hour or two attacker could lower difficulty to 1/100,000th the original value and get 5,000 blocks.
This uses the "timespanLimits" against themselves using a specific sequence of timestamps. Most coins have inherited some form of the timespanLimits from BTC. It almost always requires 51% hashrate block-withholding mining attack to have complete control of the timestamps. The result is that an attacker can get unlimited blocks in less than 3x the difficulty averaging window.
In places I may say or imply both limits are required to perform the attack. The only necessary condition to increase emission rate is a limit on how high the difficulty can rise in a block such as a limit on how short the timespan is. The converse limit may cause a decrease in the avg block emission rate.
Update: In places I mention the MTP-forced sequential timestamps in Digishield (like Zcash) prevent this attack. In fact, the asymmetrical 16% and 32% limits on timestamps in Digishield allow a 51% attack to get about 50% more blocks than the normal 100%. The process is: alternate stamps between the MTP and the value that maximizes the drop without exceeding the 32% limit. That value is the median of the last 3 in the window plus 5814 seconds which comes from (1.32-0.75)*150*17/0.25 = 5814. Alternate for 10 blocks. Then make each stamp 150 plus previous stamp for 11 blocks. Repeat the cycle however many times. The difficulty will lower but your clock will be ahead of time. End attack by setting every stamp equal to the allowed MTP. Your clock stops while difficulty rises until your clock time is equal to current time and you can end the attack.
Conceptual Overview
The timestamps in simple moving average (SMA) and BTC-type algos are selected to alternate between forward stamps that reach the upper timespan limit and delayed stamps that EXCEED the lower limit. This makes difficulty go up and down by the same amount, but by exceeding the lower limit, we can delay time which allow us to use more forward stamps to repeatedly lower difficulty, without without costing all the time we gained, eventually getting many block in little time. Direct limits on difficulty changes per block or limits on individual solvetimes per block can be similarly attacked.
Attack Specifics for SMA-type algorithms
N = blocks in difficulty averaging window
T = target block solve time
L = timespan limit which is 4x in BTC, 3x in Dash, and 2x in BCH.
Here's a quick review of a SMA difficulty algorithm:
next_target = sum_targets * T / ( timestamp[N] - timestamp[0])
The denominator timestamp[N] - timestamp[0] is limited to L*N*T and N*T/L.
A block-withholding mine that has complete control of timestamps keeps the MTP delayed by making 6 of every 11 blocks' timestamps set back to the MTP limit. This does not require the 2015/2016 "hole" that exists in bitcoin. The first timestamp ( I call it "Q") is set forward in time to drop the difficulty the most it can by setting the timestamp so that the timespan limit reached. This is M = N*T*L seconds after the timestamp of the block that is at the beginning of the averaging window, N blocks in the past. Unlimited blocks can always be obtained in less than 3*N*T (3 averaging windows). In the simple attack (that may take 2x longer) the first N=2016 blocks are just set to Q plus 1 second for each block after the block with the initial Q timestamp. The plus 1 second is because Q will soon become the MTP and the MTP rules normally require timestamps to be at least 1 second after the MTP. After the first N blocks, we start alternating timestamps between Q+i and Q+M+i where i is the number of blocks into the attack. We do not have to advance 1 second on the Q+M blocks, but it makes coding simpler at a slight cost in time. We alternate according to a specific rule: if a Q+M+i timestamp is not going to cause the MTP to increase in the next block, and if the block at the back of the averaging window N is a Q+i block, we assign a Q+M+i timestamp. Otherwise, we assign a Q+i timestamp. The chain is submitted to the public when current time equals Q+M+i. In code this simple attack is the following.
// Q = timestamp of most recent block when the attack begins
// N = number of blocks in averaging window, 2016
// M = N*T*L where L is 4 in bitcoin, the timespan limit, and T = 600.
// next_MTP = the MTP timestamp in the next block.
// At the far right in the 2nd conditional there's a vector referring to negative elements when i<N. Please
// pretend prior timestamps at those negative index locations in the vector exist (they're blocks in the past).
i=0;
if ( Q+M+i > current_time ) {
if ( next_MTP <= Q+i && next_MTP >= previous_MTP && Q+i == timestamp[i-N]+N )
{ timestamp[i] = M + Q +i; }
else { timestamp[i] = Q + i; }
i++
}
else { end attack, submit chain to public }
Code to demonstrate this attack in SMAs and others (in future)
Which coins are vulnerable? Half? Most coins have inherited a timespanLimit idea from Bitcoin which uses 1/4 and 4x. Coins that use the MTP as the most recent timestamp in their difficulty calculation are not vulnerable, but there are better options for small coins than using the MTP delay in responding to hashrate changes (MTP delay causes oscillations). Digishield coins appear to use MTP as most recent timestamp, so they are not vulnerable. [edit: Digishield coins are vulnerable if they are not using the MTP as the most recent block...I know of a big coin that has been attacked with it.] DGW coins do not, and therefore appear vulnerable. Coins that do not place limits on timespans are not vulnerable to it. Coins like LWMA that look at individual solvetimes are vulnerable if they have limits on the solvetimes.
The following type of limiting is subject to the same attack:
next_target = max(0.5*prev_target, min(next_target, 2*prev_target));
KGW (Kimoto Gravity Wave) may be even more vulnerable because it has a timespan limit here
if (PastRateActualSeconds < 0) { PastRateActualSeconds = 0; }
that prevents difficulty from rising but not a symmetrical limit to prevent it from falling.
Solutions:
timespan = median(TS[i]...TS[i-11]) - median(TS[i-N]...TS[i-11-N]) ;targetSum = sum(target[i] to target[i-N+1])// H is current block height.
// Assuming MTP=11 is used which guarantees in BTC that 11th timestamp in past is not before 12th
// This is more easily recognized as the "MTP" aka 6th block in the past if the timestamps were in order.
previous_timestamp = timestamps[H-12];
for ( uint64_t i = H-11; i <= H; i++) {
if (timestamps[i] > previous_timestamp ) {
this_timestamp = timestamps[i];
} else { this_timestamp = previous_timestamp+1 ; }
solvetimes[i] = this_timestamp - previous_timestamp;
previous_timestamp = this_timestamp;
}
prior_solvetime = solvetimes[H];
I'll describe 4 versions of this attack that use the same general idea. Only the last can be done with < 50% and requires the difficulty algorithm to have MTP/N > timespanLimit (in SMA terms).
Other problems timespanLimit causes: It causes Digishield coins to surprisingly take 500 blocks instead of 80 to reach the correct difficulty at startup, which I covered here.
Here's an old method I had of doing this attack that's not as good as the new one.
https://user-images.githubusercontent.com/18004719/43910698-898e682e-9bcb-11e8-8720-caf74d5fc495.png
timespanLimit # 2 (public method)
In public non-block-withholding mining) version, the attack first makes the MTP get way behind with a lot of MTP timestamps, raising the difficulty. He then proceeds like the block-withholding mining version of this attack, letting other miners assign the honest timestamps which are acting as "forwarded" timestamps, while he focuses on trying to maintain the MTP as old as possible, but coinciding with every honest timestamp possible as they pass out the back of the averaging window, and sometimes letting it coincide with other delayed timestamps, to make sure he maintains the delayed MTP.
Hashrate required: It requires > 90% hashrate if a coin uses the common MTP=11 and the FTL is not too large, so often it's not practical. Cryptonote coin default has MTP=60 which makes it easy, but they do not usually have a timespanLimit. It is also easier to a much smaller extent if the algorithm has short a averaging window, largish FTL/(T*N) ratio, small timespanLimits, or asymmetrical timespanLimits. It requires extremely high hashrate for smallish MTP=11 because the attacker has to get 6 of out every 11 blocks, without fail, or the attack ends and he has to start over. The following is my first pass estimate of the hashrate needed. The attack has to last at least 1.5*timespanLimit*(blocks in averaging window) to be profitable because these are the delays that result from making the MTP behind real time by the initial and necessary 2*timespanLimit*(window timespan) seconds. The smallest N for averaging windows are about 15. Some timespanLimits are 2x instead of 4x. 1.5*2*15 / 11 = 8 sequences of blocks of 11 that the attack must get at least 6 of them. 6/11 = 55%. 0.55^(1/8) = 93% in a good case scenario, not counting an advantage an attacker can gain from a large FTL/(TxN) which lowers this.
timespanLimit # 3 ( block-withholding mining on BTC-type algos)
These are the timestamps a 51% block-withholding miner can use to get infinite BTC blocks in 16 weeks.
timespanLimit # 4
The attack is easy and possible by < 50% if the % a single reverse timestamp can raise the difficulty is more than the timespanLimit. As those timestamps pass out the back of the window, the difficulty will drop more than it was allowed to raise. This is provided the limits are symmetrical or the drop limit is more than the rise limit. In SMAs, an attacker would look for MTP/N > timespanLimit. In Digishield 4x dampening: MTP/(4*N) > timespanLimit. In EMA, LWMA, and DGW types that give more weight to recent blocks, it's about 2*MTP/N > timespanLimit. Technically it's 1/timespanLimitsince it's in target.
An attacker with 25% hashrate can get lucky and find more 6 or more of the past 11 blocks, allowing him to "own" the MTP (if it's set to BTC's 11). He could forward those timestamps to the FTL limit (2 hrs in BTC). If there is an error in the template code which does not automatically give the miners timestamps similarly into the future (MTP+1), nodes will reject blocks (those with honest timestamps). Attacker could get 100% of all future blocks until other miners give their nodes a future time or fix the template-creation software. This was accounted for in BTC, but it was lost in cryptonote coins. Jagerman found the issue while tracking down Graft attacks and released a patch.
Zcash's 2/6/2020 security update could have allowed this same attack in the opposite direction by basing a new FTL limit off of the MTP but the devs knew to prevent it by having the template code use false timestamps. (https://github.com/zcash/zcash/blob/ba20384845c04fe7f3c7a585fc99d57bfccdb54b/src/main.cpp#L3829-L3840). If they had not not to enforce a dishonest stamp, attacker would have just needed to send 6 timestamps 120 minutes into the future, blocking all other miners who attempt to use honest timestamps in their templates. He can get all the blocks at low hashrate until other miners learn to give their node a fake time into the future.
In many coins like BTC, ZEC, and BCH, nodes use the median of their peers as the current time to enforce the FTL above. Coins should not use peer time because a median from peers is a consensus mechanism that does not have POW security. This allows a Sybil attack to slow a victim's network time up to the point that blocks with honest timestamps will be more than the FTL past the victim's network time, causing him to reject the blocks, at least until the block's time is in the victim's past. This allows the attacker to use bad timestamps to get accepted by the victim, enabling a double spend on the victim. If he can do the attack on a < 51% pool, he only needs half of the remaining hashrate to do a block-withholding attack to keep the blocks, and possibly do double spends on an exchange using the victim pool.
These attacks are hard to do on BTC, ZEC, BCH, etc because they revert to a node's clock time and throw a warning if median of peer time is > 70 minutes off from the node's clock. This is about 1/2 of the FTL on purpose. So the attacker can advance the victim's clock by 70 minutes before it will attempt to use its own clock, but because the FTL is a lot longer, the victim will not reject blocks with honest timestamp. So the cure is to make the revert to node time rule about < 1/2 FTL.
But it needs to be less than 1/2 FTL as Culubas's long 2011 article says. This is because the attacker might be able to do a Sybil attack on the miners' network and send the majority hashrate's time in the opposite direction regaining the ability to force the victim's node to reject the main-chain's timestamps. Attacker still needs substantial hashrate because after a while, the public chain 's older stamps will start being valid to the victim. Culubas considered the options and decided simply making the revert rule 1/4 of FTL seems to be the best.
My preference is to remove median time all together. Cryptonote who uses only the node's clock time without any problem. There was an discussion on this between kjj, kheymos, and Mike Hearn. (I agree with kjj)
Removing peer time in the above and near-perfect (+/- 1 second) local time does not eliminate the problem. An attacker with 25% hashrate could send a timestamp equal to the FTL to split the network in half and work on that tip while 1/2 the honest miners work on the older tip. His tip has 25% + 75%/2 = 62.5% hashrate the other tip has 37.5%.
After some sleuthing (with help from @h4x3rotab ), this is what I think motivated Zcash to do a security update.
The database code gets the node stuck (during reboot) by the attacker making previously-approved blocks invalid due to being in the future. A Sybil attack makes the victim nodes time go into future up to the peer offset limit (70 minutes in BTC etc). He then finds a block with a timestamp up to the normal future time limit (120 in BTC et al) plus the 70 minutes. If the node reboots in 70 minutes (can the attacker motivate a reboot?) the node can't reboot because it is not connected to the problem peer time and sees a block with a timestamp in the future.
Another attack could be to send miner nodes peer time 70 minutes into past and then find blocks with timestamps at 120 future time limit. Non-attacked nodes will approve it, but the attacked nodes will cause their miners to reject those blocks and work on a chain that will get orphaned.
Zcash's fix was to by default not allow peer time. That fixes it. But users can still select to use it. So they added a 90 minute FTL limit relative to the MTP timestamp in addition to the normal FTL=120 and limited the amount peer time can adjust time to +/-25 minutes. Or rather they make sure the constants obey 25 + 90 < 120 in case they are changed them in the future.
A typical timestamp attack is to set the timestamp of a solved block to the max future time limit (FTL) that nodes will allow. Most coins just accepted BTC's 2 hour FTL like Cryptonote, Zcash, and all the clones that came after. This was a problem because N*T in clones is a LOT lower in clones than BTC, and the amount a forwarded timestamp can lower difficulty in a single bock is
next_difficulty = average_difficulty * 1/(1+FTL/(T*N))
next_target = average_target * ( 1+FTT/(T*N) )
This attack does not cause much of a problem even with a 30% potential drop in 1 block (according to the above equation) if the attacker has < 50% of the network hashrate and the algorithm is allowing out-of-sequence timestamps and not monkeying with the math so that it the next honest timestamp is block from correcting it. If the attacker has 51% hashrate, he can start getting ahead of the honest timestamps until it has reached that amount of drop. He then starts "bumping into the FTL" and is forced to quit and let the difficulty rise back up to the correct value in N blocks, so a 51% miner on a "30% potential drop" coin (based on FTL, N, and T) gets N blocks at an average difficulty that is 15% too low from beginning to end of attack which is about N blocks. He then needs to stop manipulation for N blocks to let D rise back to normal to repeat with equal success. More likely, he will be a >3x miner who can get N/4 blocks at about 25% lower difficulty with a brief attack before moving to another coin for > N blocks.
Solution: Use FTL < N*T/10 for < 10% manipulation (lowering) of the difficulty with a single block.
This allows a >50% block-withholding miner or a 66% attack on the public chain to release more blocks than scheduled in the Homestead algo. It could be prevented with using a slightly different form for the math. See the bottom of my ETH difficulty article.
If a coin is using an algorithm that sums solvetimes instead of subtracting first and last timestamp in the window, and if it is allowing or incorrectly adjusting for out-of-sequence timestamps by using
if solvetime < 1 then solvetime = 1
(or in some cases simply sorting timestamps), its difficulty will drop to zero when a miner starts sending reverse timestamps. The negative solvetime is being ignored and the subsequent honest timestamp is being viewed by the algo as a really long solvetime because it subtracts current timestamp from that fake old one. The attacker can have significantly less than 50%. For MTP = 11 (a median at 6 blocks in past limit), it only requires > 1/6 of the network hashrate to start lowering difficulty.
Solutions:
previous = timestamps[0];
for ( uint64_t i = 1; i <= N; i++) { // N is most recent block
if (timestamps[i] > previous_timestamp ) {
this_timestamp = timestamps[i];
} else { this_timestamp = previous_timestamp+1 ; }
solvetimes[i] = this_timestamp - previous_timestamp;
previous_timestamp = this_timestamp;
}
// do algorithm with the individual solvetimes stored in solvetimes vector.
timespan = median(TS[i]...TS[i-11]) - median(TS[i-N]...TS[i-11-N]) ;This appears to be named after a 2011 GeistGeld attack described by Artforz. The only place I could find it called this is Litecoin's wiki and they have a "2" appended to the end, which I've dropped. I historically called this "the" timewarp attack and got people to say "timestamp manipulation" for other things.
The attack is not possible in any typical rolling average method. This is because it depends on a gap in the way BTC is calculating the next target. The attack is still possible on BTC, but it requires a > 50% miner.
UPDATE:
This is an executive summary for those already a little familiar with the attack. Further below has the gory details.
He needs >50% to perform a block-withholding mine so that he has control of the timestamps. He has to get at least 6 out of every 11 blocks for at least 2016 blocks to perform the attack, which requires a LOT more than 50% if it's not a block-withholding mine.
A block-withholding mine attack with only 51% hashrate would go like this:
Start block-withholding mine at end of a 2016 block cycle.
Set 2016th timestamp to 2 weeks ahead. He can do this because he has set his node to not reject the future time. Difficulty will drop to 1/3 previous value because of this.
Set at least 6 out of every 11 blocks to 1 second after the MTP for next 2015 blocks.
Since attacker has 50% network hashrate, it takes 2/3 of a week to get them.
Set next "2016th" block to same timestamp as the 1st one, 1 week into future.
Since the MTP is still delayed to only 2015 seconds after the beginning of the attack, the calculation lowers difficulty to 1/3 again, 1/9 of the initial difficulty.
He gets next 2015 blocks in 2/9 of a week.
So he's 7*(2/3+2/9) =6.2 days into the attack with 4032 blocks.
He can repeat the process to lower difficulty as much as he wants, and get as many blocks as he wants in 2 weeks.
He can't submit the chain to other nodes until real time catches up with his forwarded time (2 weeks). He must block-withholding mine the entire 2 weeks to make sure he has the most chain work.
END UPDATE
A review
BTC difficulty algorithm
next_target = previous_target * ( timestamp[2016] - timestamp[0]) / 2016 / 600
I've read there's an off-by-one error which may mean the timestamp[2016] is actually 2015, so the numerator may be 2015 solvetimes from the subtraction of 2016 timestamps instead of 2016 like I have it, so the result of the error would be that next_target is 1/2016 too low.
Here is a restatement of the equation to show by intuition that it should work. if avg solvetime was 50% too high, it raises target 50%, making it 50% easier (2x higher difficulty)
next_target = previous_target * average(solvetime) / target_solvetime
For reference, a simple rolling average difficulty algorithm is basically the same thing, except that it can change every block.
SMA difficulty algorithm
next_target = avg(target) * avg(solvetime) / target_solvetime
I'll more fully explain ArtForz's description of the GeistGeld attack and shamelessly steal his example.
Let's say we have a chain with 3-block difficulty window instead of 2016, and target solvetime is 10 sec/block, and miners just happen to get all the blocks in exactly the target solvetime. So blocks would come in like this:
blk number 1 2 3 4 5 6 7 8 9 10 11 12
timestamps 0 10 20 30 40 50 60 70 80 90 100 110
The old BTC algorithm with a 3-block window is: (ignoring integer math round off error)
next_target = prev_target * (timestamp[4] - timestamp[1]) / 3 / 10
I've called this a 3-block window but Artforz incorrectly called it 4-block. The (timestamp[4] - timestamp[1]) is only 3 solvetimes. For the above 10-sec solvetimes, next_target will be the same as previous target because all the solvetimes were the target solvetime (it does not need an adjustment).
The problem results from how one calculation of it does not begin exactly at the end of the previous calculation. It uses (timestamp[9] - timestamp[5]) instead of (timestamp[8] - timestamp[4]). The problem is that there's a solvetime not being accounted for. The solvetime (timestamp[5]-timestamp[4]) is missing. Someone figured out how to exploit this.
I'm going to describe this as a block-withholding attack with a >50% miner, but enough hash power and lucky enough to always get at least 6 out of every 11 blocks for the entire 2016 blocks he can do this so that the difficulty is lowered for everyone. He could hold the median of the timestamps to increase only the minimum of 1 second per block, and then avoid setting the 2016th block to that delayed time (otherwise difficulty would jump (target would fall) to the max of 4x (1/4 previous target)), and be sure to get the 2017th block and set it to that delayed time which is only 2017 seconds after the previous week's final block instead of the real time which would be about 2016*600 seconds afterwards. Then he just needs to sit back for a week for the next adjustment which will drop to 1/4 of the previous difficulty (4x higher target).
Imagine a big miner with > 50% network hashrate starts block-withholding. He could assign timestamps like this
blk number 1 2 3 4 5 6 7 8 9 10 11 12
timestamps 0 1 2 30 4 5 6 70 8 9 10 110
Note that most of his timestamps are assigned into the past. 30, 70, and 110 are the only correct timestamps. The MTP limit on past times will not stop this because the correct time coming once every 4 blocks will never be the median of the past 11. The FTL limit will not stop it because the miner doesn't need a node to approve it, and if he's using a node to send the block template, then he's changing the time on it to generate the above times, so of course the node will agree with itself.
The attacker's "sum of solvetimes" for the next_target numerators are:
first period (#4 - #1) is 30s as before => next_target = prev_target
2nd period is (#8 - #5) ... 66s => next_target = prev_target * 66/30
3rd period is (#12 - #9) ... 104s => next_target = prev_target * 104/30
So by the 3rd calculation, the target has risen 66/30*104/30 = 7.6x higher (easier) when it was supposed to be the same (for this example). In reality, if he had 51%, the first solvetimes would have been 2x too long, so target would have risen 2*7.6 by the 3rd calculation.
So the >50% miner can have all the blocks he wants in less time than the network has had to go through about 6 target changes.
When he decides to submit the chain to the network, he will make his final timestamp correct so nodes checking it against current time (within FTL limit) will not see a problem and approve it. They can't check prior blocks against current time.
If he has more than 50%, and his final blocks get back to current time, he will have more chain work by whatever proportion he was over 50% of the network hashrate, which is not related to how many blocks he gets or what the difficulties were. His advantage is that there will be many more blocks he's solved. Artforz indicates he needs to assign 1 second solves to make difficulty rise high at the end in order to win chain work, but that's not correct. It can't help him to get the highest chain work if he has < 50%.
Let's say a 51% miner who's been mining BTC starts block-withholding right before a difficulty change, below the underline shown below. As he starts to block-withholding, the rest of the network is going to take 2x longer to find blocks because he has left.
T = target solvetime = 600.

But because of the timestamp he's assigning, he's not going to have delays. Notice that his final timestamp matches real time so that he can then submit the chain to the network. Notice that he got all 2*2016 blocks in the two weeks he was block-withholding, while the network only got 2016, which they now have to discard. Despite having 2x more blocks, his total work is only 1% more than the public chain, which is the only reason he needs to have > 51%.
Red is the last block of a window, and blue is the 1st block. So the solvetime in the equation is red minus blue timestamps.

[1] 1993 "The Consensus Problem in Fault-Tolerant Computing" Barborak, Malek
"What must be recognized is that each of these [consensus] layers is a separate consensus problem. First, the synchronization level maintains a global timepiece which is simply a consensus of all the processing elements [nodes} on a particular time value and a rate of change of that value."
[2] 1978 "Time, Clocks, and the Ordering of Events in a Distributed System" Lamport
Conditions IR2 and IR2' require sequential stamps on messages. This paper requires all events (change of state) to increase (no reset of a clock to be before a previously-ordered event). In the case of Nakamoto consensus, this means new timestamps on blocks can't be set to before validated timestamps on prior blocks. Block height is not relevant because a faster sequence of timestamps can override previous height ordering because it indicates a higher hashrate ("participation rate of voters"). "Timestamps used to count participation" was the key discovery of Nakamoto consensus that seemed to do the impossible. Timestamps count hashes via the difficulty setting and hashes are the sum of all events in all mining nodes for Lamport ordering that all nodes can estimate from how fast blocks are and the difficulty setting. A negative solvetime (non-sequential timestamps) has been used many times in different ways to attack the consensus on coins because it exaggerates the estimate of hashrate. Prior proofs assumed nodes would use agreed-upon start and stop times to measure participation, but Nakamoto consensus does it sort of backwards, using time itself to count participation.
[3] 1982 "The Byzantine Generals Problem", Lamport, Shostak, Pease. p398-399
The sender and receiver [must] have clocks [or equivalent time-out procedure in voting] that are synchronized to within some
fixed maximum error. .....
We therefore have the problem of keeping the processors' clocks all synchronized to within some fixed
amount, even if some of the processors are faulty. This is as difficult a problem as the Byzantine Generals Problem itself. Solutions to the clock synchronization problem exist which are closely related to our Byzantine Generals solutions. They will be described in a future paper.
The future paper was in 1984 "Byzantine Clock Synchronization" which is vulnerable to normal Byzantine attacks (>33% or >50%). It doesn't make sense (it's circular reasoning) to try to use another POW for the clock to secure POW (unless it's turtles all the way down). POW consensus is only as strong as the consensus mechanism on the clock, so no consensus mechanism should be used.
[4] 1988 "Fault-Tolerant Clock Synchronization" Halpern, Simons, Strong, IBM Research
Takeaway: ETH's new DA for Homestead works exactly like a good EMA despite only adjusting in tranches, enabling its use in situations where difficulty (timestamp) grinding may be a problem. It allows 75% more blocks than normal if there is a selfish mining attack. A safer version of it can prevent this. After inverting the ETH algorithm to prevent a problem described below, the similarity between EMA, ETH, and Digishield can be seen as follows. Where Digishield's N is a lot smaller because avgST is a lot more stable than ST.
// Similarity between algorithms
// Floating point math except for int().
// ST = solvetime for previous block
// T = target solvetime
// N = factor to slow down speed of response.
EMA_Target = prevTarget * ( 1 + ST/T/N - 1/N )
ETH_Target = prevTarget * ( 1 + int(ST/T/ln(2) )/N - 1/N ) // ETH's Homestead after fixing it.
Digishield_Target = avgTarget * ( 1 + avgST/T/N - 1/N )
ETH's actual code and explanation are here and here. I use floating point here for clarity.
ETH's original DA in the Frontier release used the simplest possible DA that says "if solvetime was fast, increase difficulty by a small percent, else if it was slow decrease it by same amount."
// ETH's Frontier DA
if (solvetime < 13) { D = priorD*(1.0005); }
else { priorD*(0.9995); }
This simulates more complicated algorithms such as SMA's (including DGW) and Digishield but the small correction factor means it's a lot slower than most algorithms. The newer ETH algorithm is a "discrete" simplified EMA, which they seem to have come across by intuition and experiment. BTW, ETH's and EMA can't be used in coins like Cryptonote clones which simply assign the completion time of the previous block as the timestamp of the current block. It results in substantial oscillations.
ETH's Frontier DA does not result in a 13-second avg solvetime because half of a Poisson distribution's solvetimes are < ln(2) = 0.693 of the target solvetime. So the above results in an average 13/0.693 = 18 second solvetime.
A problem occurred with miners assigning only +1 second timestamps so that if there was competition with a simultaneous solve (15-second solvetimes will have a lot of "collisions" in solves due to propagation delays) the miner wants his block to win by having a very slightly higher chain work by claiming his solvetime was a lot faster than it was. This did not change the median solvetime, but the mean solvetime could increase a lot especially if >51% of miners did it. To quote devs for the new DA:
The difficulty adjustment change conclusively solves a problem that the Ethereum protocol saw two months ago where an excessive number of miners were mining blocks that contain a timestamp equal to parent_timestamp + 1; this skewed the block time distribution, and so the current block time algorithm, which targets a median of 13 seconds, continued to target the same median but the mean started increasing. If 51% of miners had started mining blocks in this way, the mean would have increased to infinity. The proposed new formula is roughly based on targeting the mean; one can prove that with the formula in use, an average block time longer than 24 seconds is mathematically impossible in the long term.
The new DA does not stop them from assigning +1 timestamps, and doing so still has the effect the miners desire, but now they can assign anything <10 seconds to have the same effect so they do not need to skew their solve time as much. It only fixes the mean solvetime. However, their fix allows the opposite potential harm of faster average solvetimes as the bottom "attack" section shows. The new DA is
// ETH's Homestead DA
// ST = solvetime as reported by miner
D = priorD * ( 1 + 0.0005*(1-int(ST/10) )
// General form:
// T= target solvetime
// N = "window size" (aka slowness aka stability factor)
D = priorD * ( 1 + 1/N*(1-int(ST/T/ln(2)) )
// to see this more clearly:
if (ST < 10) { factor = 1.0005 } // ST too fast, increase D.
else if (ST < 20) { factor = 1 } // ST about right, do nothing.
else { factor = 1-0.0005*int(ST/10) } // ST too slow, decrease in proportion to slowness.
D = priorD*factor
This method with constant hashrate has an theoretical (experimental with constant hashrate) average solvetime just below 15 seconds.
Making ETH's Frontier as fast as Digishield
Digishield's math "dilutes" the effect of its solvetimes by 4, so its window of 17 blocks acts like an improved SMA with N = 17*4 = 68. Digishield responds quickly due to the 17 but the response is moderated by the dilution factor of 4. For a given speed of response to typical hashrate changes < 10x, it is smoother than SMA, which makes it overall a lot better, but for sustained changes in hashrate it is a lot slower, taking 500 blocks to reach the correct difficulty after genesis. Since ETH changes per block, 1/68=1.5% indicates ETH's simple method can simulate Digishield with 1.5% per block changes. Experimentally I see 2% looks very much like Digishield.
Digishield is this:
// Digishield
// Ignoring the fact that the solvetimes are shifted MTP (~6) blocks in the past.
// T = target solvetime
// ST = solvetime
nextTarget = avg(17 prior Targets) * ( 0.75*T + 0.25*avg(17 prior STs) ) / T
// In terms of difficulty the following can be used, but to be exact
// use the harmonic mean of the prior Ds instead of average.
D = avg(17 prior D) * T / ( 0.75*T + 0.25*avg(17 prior STs) )
// Notice that rearranging & using the approximation 1/(1+x) =~ 1-x for small x
// can show a similarity between Digishield and ETH. x isn't very small for Digishield here,
// but it's not going to be > 0.5 very often. In testing under various conditions, I could not
// determine which of these forms of Digishield was better. Note that avgST is a lot more
// stable than ST, so the 25% adjustment factor can be a lot bigger.
D = avgD / (1 + [-0.25 + 0.25*avgST/T] )
// apply 1/(1+x) =~ 1-x approximation
D = avgD * (1 + 0.25*[1 - avgST/T]) // "inverted Digishield"
ETHs Frontier algorithm can do a good job of simulating Digishield by changing 2% per block instead of 0.05%
// ETH's Frontier with 2% instead of 0.05% jumps per block
D = priorD * (1.02 if ST< T/ln(2) else 0.98)
// or in terms of target:
nextTarget = priorTarget * ( 0.98 if ST< T/ln(2) else 1.02)
Comparing ETH's Frontier to Digishield
The above two difficulty algorithms look so identical when hashrate is constant, I'm not even including the plots. Both have about 0.11 Std Dev (trying to get the same value is how I chose 2%). The charts below compare them with 1.6x hashrate attacks that start when difficulty falls below average and stop when it is 10% above average. The "delay"and "blocks stolen" metrics appear worse for this modified ETH Frontier DA (aka 2% change per block algorithm), but some of it is because it is being subjected to more attacks as a result of getting back to the correct difficulty faster. Also, the average solvetime is 3% higher than target under this miner-motivation scenario while Digishield will remain accurate under all conditions. All algorithms can appear better to the degree the solvetime is allowed to be compromised. In short, Digishield is definitely better, but a casual view of the charts can't see much of a difference. These charts are 1200 blocks.
2% jump refers to ETH's Frontier algorithm with a much faster "response speed constant".
Comparing ETH's Homestead to Digishield
The above 2% Frontier algorithm can be modified to give a fast version of ETH's Homestead. I'm not including the max(x, -99) rule because it will not occur in normal circumstances. Homestead gives higher weight to longer blocks, enabling it to drop faster after long delays. This would seem to make the average solvetime faster, but the average solvetime stays accurate (like Frontier) because solvetimes (STs) from 0.693T to 20.693*T do not decrease difficulty as they do in Frontier. It's surprising this simple method still gives a pretty accurate target solvetime T.
// modified 2% jump DA
// This is a fast version of ETH's Homestead DA.
D = priorD * ( 1 + 0.02*(1-int(ST/T/ln(2)) )
It looks more unstable than Digishield with constant hashrate as shown below, but the Std Dev in difficulty is the same. The small error in average solvetime is an offset error that can be easily fixed by a slightly higher T.
mod 2% jump refers to ETH's Homestead algorithm with a much faster "response speed constant".
It has the same response speed to increases in hashrate as the previous 2% jump algorithm, but it falls a lot quicker after attacks. In one sense this might make dedicated miners happier, but it can result in more oscillations if the attacker keeps coming back ASAP as the chart below shows. Homestead looks worse than Frontier, but this is all because of the method of testing. A new attack begins a lot more quickly because the difficulty dropped. Notice that despite more frequent attacks the metrics are the same. And the avg solvetime is low, which means it can be modified to make the attacks less frequent. So the Homestead algorithm is better than Digishield. My next example will make it more apparent.
Comparing ETH's Homestead to EMA
I have long been a fan of the EMA difficulty algorithm which I explore in issue 17
It turns out that ETH's new DA is exactly a "discretized" version of the simple EMA. The EMA is a modified version of the exponential moving average used in stocks. The simple EMA uses the approximation e^x =~ 1+x for small x (as the link to issue 17 above details).
// Simplified EMA (JE's EMA)
// A continuous version of ETH's Homestead DA (this is floating point math)
D = priorD * (1 + 1/N*(1 - ST/T)
To get DAs on equal terms when comparing their speed of response to hashrate increases, I first adjust their main parameter ("window size" in most DAs) to have the same Std Dev stability to a constant hashrate. Doing this to make the simple EMA like the 2% method above, I needed N=35 for the EMA. This results in:
// Simplified EMA to compete with Digishield and mod 2% jump (continuous ETH)
// N = 35
D = priorD * (1 + 0.0285*(1 - ST/T)
To my surprise, the simple EMA is indistinguishable from ETH's homestead. The following is a more typical attack scenario seen in Zcash clones using Digishield than the example above, this time using a 3x attack starting when D is a little below average and stopping when it has risen 30%.
Timestamp Attacks on ETH
The ETH and mod 2% DA shown above should not be used. They allow for the possibility of negative difficulties (e.g. if ST is a very long 36xT in my 2% version of Homestead). If that is patched as in ETH with a max(-99), a private mining attack can still get an excess of blocks, above and beyond a normal selfish mining attack. ETH's is strongly protected with the small 1/2048 =~ 0.05% change per block and max(-99), but an attacker with > 50% can still do a selfish mine and get 75% more blocks than the public chain. He can do this by assigning timestamps 1000 seconds apart for 60 blocks then assigning +1 timestamps for the next 7720 blocks and then send the chain to the public network. Attacker gets 7780 blocks while the public chain gets 4450 if attacker has only 51% (a hashrate equal to the public chain). If his profit margin is normally 50%, he makes 7780/(4450*0.50*0.51) = 7x more profit from this attack.
For the same reason, if 66% of ETH's public miners assign +1 timestamps, solvetime will reduce to 11.5 seconds, causing too many blocks per time to be issued.
Most coins need a faster response to hashrate (2% change per block instead of 0.05%) which can be more easily attacked with greater damage than the above because max(-99) can't be used. The smaller the 99/2048 ratio, the less the attack can profit. But with N=35 instead of 2048, that would block the 1.75xT solvetimes.
The best way to stop this attack is to use the simplified TH-EMA, or the accurate JE-EMA. I've shown how they can be discretized.
// Simplified TH-ema
// floating point for math clarity
D = priorD * N / (N+t/T-1)
// Inverted form of ETHs Homestead to protect against attacks & negatives
// Same as the Simplified TH-EMA above, but "discretized"
D = priorD * N / (N+ int(t/T) - 1)
// *********
// Same as above with integer math. This is the algorithm people
// should use if they want ETH's Homestead without the problems.
// The more complicated version at bottom might be more accurate.
D = (priorD*N*1000/( N+ int(t/T) - 1) ) /1000
// **********
// Accurate JE-ema (floating point for clarity)
k = t/T/N
D = priorD * (1+1/N+k*(k/2-1-1/2/N))
// ETH's Homestead non-inverted & more precise to prevent
// negatives and attacks. This is floating math for clarity.
k = int(t/T)/N
D = (same as above)
// Same as above, but in integer math:
// N<100 for <1% error
// D might overflow in some coins
k = 1E4*int(t/T)/N;
D = (priorD * (1E8+1E8/N+k*(k/2-1E4-1E4/2/N)) ) / 1E8
MM problems:
In general it just seems to cause problems by having dis-interested miners mining the coin. But it keeps coming up as a potential important way to prevent 51% attacks that result in double spends on exchanges..
See also this.
This shows the performance of 7 coins' difficulty algorithms for 3800 blocks. Notice in the additional posts below that Masari's with the new WHM N=60 is doing better than the runner-up (Zcash) ever did in the past year.
I would like to investigate other coins with other algorithms. See please send me your coin data to include your coin here.
The "% blocks 'stolen'" aka "cheap blocks" aka "hash attacks" is "blocks suddenly obtained with a high hash rate as evidenced by fast solvetimes in excess of the expected fast solvetimes". It is approximately 2x the avg of 11 ST < 0.385xT, so it is like the converse of the other metric "avg 11 SolveTimes > 2xT".
"Delays" are "avg of 11 ST > 2.1xT" and the >2.1xT values are printed on the charts. The values are divided by 4. For example, an avg 11 ST = 3xT is 3/4=0.75 on the charts. A 3x baseline hashrate attack is also 0.75.
The average 11 ST includes a lot of logic to prevent out-of-sequence timestamps from throwing off the calculation for the two metrics.
See also
the best difficulty algorithms
how to choose N for the averaging window
methods for handling bad timestamps
introduction to difficulty algorithms
CryptoNote coins do not normally have a bits field or "maxTarget aka "powLimit" aka "leading zeros". This means difficulty = avg number of hashes needed to find a solution.
CN difficulty = 2^256 / target
CN hashes needed for 50% chance of winning = difficulty
CN hashrate needed for 50% chance in solvetime = difficulty / targetSolvetime
Bitcoin / Zcash / etc
In order for a 256-bit hash to be valid (i.e. the miner finds winning block), it must be less than the "target" value encoded in nBits. A 256 bit hash has equal likelihood of being any of the 2^256 possible values. Miners change the nonce and compute the hash until a hash less than the target is found. If the target is 2^216 =~ 1.05E65 (the 217th bit from the right (least significant) is 1 and the rest of the bits are zero), it is expected the miner will need to compute 2^256/2^216 = 2^40 =~ 1.1 trillion hashes to encounter a hash lower than the target. This 2^256/target number of hashes expected is the actual difficulty which is what I refer to in all my articles. The reported difficulty of BTC, Zcash, etc scales the actual difficulty value down with a powLimit factor (aka maxTarget) that replaces the 2^256 in the numerator of the actual difficulty. I don't know of any useful purpose scaling down serves, but the code does not allow difficulty to get easier than powLimit. In BTC and Zcash this value is:
BTC: powLimit = uint256S("00000000ffffffffffffffffffffffffffffffffffffffffffffffffffffffff");
ZEC: powLimit = uint256S("0007ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff");
This is hex, so each digit represents a nibble (4 bits), so BTC's powLimit starts with 8 zero nibbles, or 8*4=32 "leading zeros" of bits. Zcash's "7" nibble is 0111 in bits, so Zcash has 3*4 + 1 = 13 bits of leading zeros. All this means that when BTC and ZEC have an actual difficulty of 2^256/target, they report the difficulty powLimit / target which is 2^(256-x)/target where x is the number of leading zeros. In other words, the actual difficulty (number of hashes expected) is 2^x times more the reported difficulty.
But these are not exactly the reported difficulty (there's a 1/65,500 difference in BTC and 1/500,000 in ZEC) because powLimit is converted to the "nBits" encoding format before the powLimit/target calculation is made. The target is also converted (compressed) to this format after the difficulty algorithm calculates a value. The encoding truncates all but the most significant bits of targets and powLimit. The compressed powLimit values in nBit format are:
BTC:
nBits-encoded powLimit = uint256S("00000000ffff0000000000000000000000000000000000000000000000000000");
ZEC:
nBits-encoded powLimit = uint256S("0007ffff00000000000000000000000000000000000000000000000000000000");
Instead of trying to spend a lot of time explaining how the nBits encoding converts 256-bit values to 4 bytes (like here, here, and here ), I'll just show the math. In the following the left-most hexadecimal is in the nBits format. The 1D & 1F are the exponents (number of bytes in the encoded number) and the 00FFFF and 07FFFF are the mantissa.
BTC powLimit:
1D 00 FF FF = 256^(0x1D - 3) * 0x00FFFF = (2^8)^(1*16+13 - 3) * 65,535 = 2^208 * 65,535
ZEC powLimit:
1F 07 FF FF = 256^(0x1F - 3) * 0x07FFFF = (2^8)^(1*16+15 - 3) * 65,535 = 2^224 * 524,287
The "-3" is because the 1D and 1F exponents include the 3 bytes in the mantissa, so they need to be subtracted when using it as the exponent. The highest bit of the mantissa for the encoding is supposed to be used to indicate sign and this is why BTC's powLimit is not 1C FF FF FF. It's a mess for no reason. Satoshi should have used 2 bytes instead of 4 where the first byte is the exponent indicating number of bits and the 2nd is the mantissa that would have 256 levels of precision for a given exponent.
The target for each block is encoded in the 4-byte nBits aka "bits" field in the block header. Some block explorers simply (stupidly) convert the 4 bytes of the hexadecimal nBits to a decimal "bits" field that makes no sense. It goes up & down with target in the right direction, but the scale makes no sense. You simply convert it back to hexadecimal to get it in the nBits format. Here are two nBit target values for BTC & ZEC and how to precisely calculate the reported difficulty that block explorers show with just a calculator:
BTC:
nBits target = 17 5D 97 DC = (2^8)^(0x17-3) * 0x5D97DC = 2^160 * 6133724
difficulty = powLimit/target = 2^208 * 65,535 / 2^160 / 6133724 = 2^48 *65,535/6133724
ZEC:
nBits target = 1C 01 0B 13 = (2^8)^(0x1C-3) * 0x010B13 = 2^200 * 68,371
difficulty = powLimit/target = 2^224 * 524,287 / 2^200 / 68,371 = 2^24 * 524,287 / 68,371
Again, this is not the actual difficulty miners have to solve. They just have to find a hash that is less than the target which is a difficulty (expected number of hashes) equal to 2^256 / target.
See also bitcoin wiki on difficulty
bdiff = difficulty
pool difficulty = 256/255 * difficulty
As an interesting idea, BTC / Zcash clones could change their max powLimit to 2^256 / block_time so that hashrate is equal to the reported difficulty. The primary goal of difficulty algorithms is to estimate hashrate to set the difficulty so that the average solvetime is correct, so it should be the best-available estimate of hashrate.
The goal of a difficulty algorithm is to estimate the current network hashrate (HR) to set D so that on average it will take the network the target solvetime (T) to find a solution. [update: if a difficulty algorithm can be made to reduce switch mining that causes oscillations in solvetimes, the average confirmation time will reduce to the avg solvetime so that is another desirable goal. Another goal could be to make the distribution of solvetimes more spread out than the exponential so that there are fewer orphans or so that block time can be reduced. See footnote. ] Difficulty algorithms only seek to set the difficulty according to:
D = HR * T / 2^x
where HR=network hashes per second and x is the number of leading zeros the code uses to scale D down.
[ update: for a more complete derivation of a fixed-window difficulty algorithm see Correcting BTC's difficulty algorithm ]
**[ update # 2: the almost perfect correct difficulty algorithm is ASERT:
next_target=previous_target * e^[(t/T-1)/N] ]
The only way to know the current network HR to solve for D in the above equation is to see how long it takes to solve blocks for previous D's. Rearranging the equation and changing T to observed solvetimes (ST) , we can measure HR of a single solve:
HR = 2^x * D / ST
where ST=solvetime. So we get an HR for the previous D and ST and plug it into the previous equation to get the needed D for the next block. There are two big problems with this. First, there is a huge variation in each ST. Secondly, there is a 50% chance that this single measurement will be < 0.693 of the correct HR because the probability distribution of a Poisson process is skewed low. ( The median is ln(2)=0.693 of the mean. ) So the HR will constantly jumping too high, > 1/0.693 too high half the time.
Naively, I first tried to determine HR by
Arithmetic Mean
HR = 2^x * avg(Di/STi) = horribly wrong
Closer would be the
Harmonic Mean
HR = 1 / avg( STi / (Di * 2^x)) = 1/ avg(STi) / avg(Target) = good but still wrong
The more accurate method is this:
Weighted Harmonic Mean or Weighted Arithmetic Mean
HR = 2^x * avg(Di) / avg(STi) = 2^x * sum(Di) / sum(STi) = better but not perfect
For whatever reason, the following needs less of a correction factor to have a more perfect avg solvetime when used to set the difficulty:
HR = 2^x * harmonic_mean(Di) / avg(STi) = better but not perfect
Note that harmonic_mean(Di) = 1 / avg(target/2^(256-x)), so that algorithms which average target instead of difficulty are calculating harmonic_mean(Di). This seems to give very slightly better results in algorithms like LWMA that depend on individual D/ST values.
I'll use velocity as an example to show how having to choose the right averaging method is a common problem that's not specific to our Poisson distribution. Let v = a velocity analogous to HR. Let d=distance like difficulty and t = time per distance like solvetime per difficulty.
If you change velocity every fixed interval of time and record the velocity in each fixed t, then your average velocity is:
avg_v = avg( v ) Arithmetic Mean
If you change v every fixed d (like mile markers) and record only velocity you have to use:
avg_v = 1/ avg(1/v) Harmonic Mean
If you have velocity but are measuring it in non-equal intervals of either distance or time, you use either the Weighted Arithmetic Mean (if we have a different ti for each vi) or the Weight Harmonic Mean (a different di for each vi):
avg_v = sum(vi * ti) / sum(ti) Weighted Arithmetic Mean
avg_v = sum(di) / sum(di/vi) Weighted Harmonic Mean
But our case with difficulty is that we don't have hashrate (velocity) and a choice between D or ST. We have D and ST. Notice that if you likewise do not have velocity data directly, but have d and t, then two weighted means are equal:
avg_v = sum(di/ti * ti) / sum(ti) = sum(di) / sum(di/(di/ti))= sum(di) / sum(ti)
Although we look at it piecemeal when we're gathering the data, we don't need to know which d was associated with each t because velocity = total_d / total_t. This is what we need for difficulty.
So we have:
HR = 2^x * avg(D) / avg(ST) = 2^x * sum(D) / avg(ST)
For a given rolling window of size N, we have:
HR = 2^x * sum(N Ds) / sum(N STs) = 2^x * avg(D) / avg(ST)
We call this a simple moving average (SMA) although it is a weighted mean as explained above. Plug this into our 1st equation that describes the goal of a difficulty algorithm:
D = HR * T / 2^x
and we get a basic SMA difficulty algorithm:
where "adjust" is needed for small N and I have determined it via experiment with a modeled constant HR and confirmed this equation on live coins from N=17 to N=150:
adjust = 1/ (0.9966+.705/N) for 10<N<150
and just leave it off for N>150. Values of adjust at N=15, 30, 60, 120 are 0.958, 0.98, 0.992, 0.998. I do not know if this adjustment factor is needed because of the skewed Poisson, or if it is the result of the equation being recursive: past D's affect future D's. A largish variation in HR requires a slightly larger adjustment (the adjust correction value is smaller), but it can't be calculated unless you do an adjustment based on the StdDev of the D.
There is also the average target method (harmonic mean of difficulties) to replace the numerator in the above which does not change the results except the adjust factor is closer to 1 which implies this method is more correct.
For small N, there will be a lot of error in this next_D calculation. You can "expect" it (aka 1 StdDev) to vary roughly by +/- 1.3/SQRT(N) and generally the result will be within +/- 2.6/SQRT(N).
The above SMA algo has a problem. We want to set D based on current HR but it gives the average hashrate as it was N/2 blocks in the past. So we want to somehow take the slope into account. We need to look at individual values of D and ST despite the errors above. When averaging discrete values, the simple harmonic mean above is a LOT more accurate for HR than the arithmetic mean because the ST varies a LOT more than D. It's like we are assuming D is fixed which is when it should be used. That is what the best algorithms do. An exception is the tempered SMA of Digishield v3. It acts like a better version of an SMA with N=60. It averages only very recent blocks, but tempers how much those recent blocks an increase it. In a weird way it is like taking a slope into account. Its equation (without the Digi v3 problems is:
next_D = T * sum(N D) / [0.75*N*T + 0.2523*sum(N ST) ]
This is a really good algorithm with N=17, if the problems are removed from the code. It usually invites fewer hash attacks from random variation at a cost of more total blocks with post-attack delays. I changed the 0.25 in the algo to 0.2523 to get avgST more precise. Experimentally and in Zcash and Hush avg ST was 0.2% to 0.5% too high.
The EMA takes slope into account and amazingly needs no correction factor, even if HR varies a lot.
next_D = previous_D * [T/ST + e^(-2*ST/T/N)*(1-T/ST) ]
Due to the impossibility of getting the exact current HR, we have to make a choice. To get the most recent estimate, we have to use a smaller N which causes more accidental variation. We have to choose between "stability" and "recency". We end up needing to consider miner profit motives:
Miners seek the highest (coins/block*price+fees/block) / (difficulty*2^x).
For a given coin, this approximately proportional to (Coin Price)/Difficulty. If price jumps 25%, about 300% more hash power jumps on which needs the algorithm to respond quickly. But if you make N too small, your difficulty will exceed 25% changes by itself from random variation, causing the Price/difficulty to be as attractive to miners as if the price jumped 25%. This means.....
**[ This section is outdated. ] **
(#14). My best guess at the best value for N (as it is used in SMA, WHM, and my version of EMA) is
T = 600, N=40
T = 300, N=60
T = 150, N=80
T = 75, N=100
Which by an equation is:
N=int(50*(600/T)^0.33)
Miners choose the block's timestamp which causes confusing problems for difficulty algorithms. See handling bad timestamps. Miners could send difficulty very high or low or cause nodes to crash (e.g. divide by zero or computing a negative difficulty) if the algorithm does not handle timestamps correctly. There's not a way for the same code to work in all algorithms. SMA's that subtract first timestamp from last have to do something different from SMAs that loop and the WHM. The EMA has to use a 3rd method.
Simply assigning solvetime=1 or 0 when a timestamp is out of sequence causes a catastrophic exploit in the EMA, WHM, and SMA's that loop. A >15% hash rate miner can send your difficulty to zero indefinitely. But realistically the low difficulty would attract so much more hash power from other miners who are not doing it, that the exploit is limited.
If the goal of difficulty algorithms is to find the current hashrate and set difficulty accordingly, then it is different from processes that need a PID controller. The algorithms do not look at an error signal of where the system is and where we want it to be and then set the next D accordingly. We measure HR and set D for that HR. Mining and solvetimes also do not seem to have a "mass" aka momentum, so they can't be modeled and controlled like the the typical 2nd order differential equation of typical physical systems. Miner motivation suddenly increases and decreases based on price/difficulty ratio, so even if we somehow control based on that, it's not a linear equation necessarily could be correctly controlled witha typical PID controller. Also, miners are active agents seeking profit who will change their behavior based on the controller. So in PID terminology the "plant" changes as soon as you devise an optimal controller for it. But I'm trying see if the PID control ideas might help.
The median of a Poisson (solvetimes) is ln(2)=0.693 of its mean.
The StdDev of a Poisson is same as its mean.
To simulate solvetimes:
ST = D * 2^x / HR * (-ln(rand())
D = (2^256-1)/(nBits as target).
Probability of a solvetime < t
CDF = 1-e^(- λ*t)
where I assume the difficulty is correct, so λ = 1 block per T which gives
CDF = 1-e^(- t/T)
Probability of a solvetime > t
e^(-t/T)
Histogram is derivative of CDF aka the PDF or PMF, i.e. λ exp(−λt). For example T=600, 10,000 blocks, and histogram bins = 5 seconds, then use the following to generate the histogram:
block count / 5 seconds = 5*1000*(1/600)*e^(-t/600)
Use CDF to predict orphan rate to an estimate of network delays, assuming there is no 1-block selfish mining and network can be modeled as two nodes with 50% hashrate each and there is a network delay between them.
orphan rate = 1-e^(-delay*2/T)
Probability P of seeing M blocks in X time when the true average is N blocks:
P = N^M/M!/e^(N)
Repeat the above for values > or < M and sum them all to get the total probability of seeing "M or more" or "M or less".
Addendum you probably want to ignore
An good approximation instead of the summing loop to get P (for M and above or M and below) is to treat the M sample as if it were continuous. If the Poisson were continuous, the M sample would exactly follow a Gaussian, which is why this is close enough for most practical purpose. Start with the basic equation:
M = N +/- StdDev * SQRT(N) eq1
For example, 95% of the time, M will be within N +/- 1.96*SQRT(N). StdDev=1 is the "expected" deviation (68.2% chance a set of M is within the range indicated). Divide both sides by N and you can say the percent error expected is within +/- 100%/SQRT(N). Since difficulty is mostly 1/avg(ST), this is also approximately the error in difficulty algorithms that act like an SMA of size N. The error is actually a bit larger.
Side Note: I use this to estimate the behavior of difficulty algorithms. I have to multiply the StdDev by a constant k of something like 1.1 to 1.5 depending on the level of probability, the algorithm (SMA, EMA, WHM), and if I'm looking at the higher or lower limit.
D variation estimate = D*(1 +/- k*StdDev*SQRT(N) )
Getting back to the goal of finding P of the found blocks being above or below some M: Instead of using a chart to look up probabilities for the StdDev in the above, use:
StdDev = (2.48*LN(0.69/P))^0.5-0.91
where P is same as above (1 tailed and not 2-tailed as is typical in charts). Rearranging and combining the two equations gives:
Probability of finding M or more (or M or less) blocks when the true average in that given time period is N.
P = 0.685\*e^(-0.81\*[ABS(M'/N-1)\*(N/2)^0.5+0.64]^2) eq2
The "ABS()" corrects it to be able to use > or < M correctly. Use M'=M+0.5 for M and below, and M'=M-0.5 for M and above (shift by 0.5 to towards the mean in both cases). You can find cases where this has a lot of error such as small N and unlikely events (e.g., N=10, M=2 gives 0.009 when it should be 0.003) but these cases are also the ones where the luck of finding 1 extra block or not makes a huge difference.
It would be nice to calculate the range of avg of M solvetimes to be expected with at a given P in order to get a general equation for detecting hash attacks based on an M-sample of blocks. But I can't. I have to select specific criteria like "avg 11 STs > 2xT" and then experimentally test to see how rare this is. To show why I can't do it by theory for a general equation, I start by dividing eq 1 on both sides by X to get M/X = 1/avgST on the left and substitute N = X/T expect blocks in X, then invert both sides to get the range for avgST that I wanted. This gives
avgST of M blocks in X time = X/M= T/(1 +/- StdDev*SQRT(T/X) )
This is a problem because I need SQRT(T/X) to be a constant and X will vary. This is why it only works only in very restricted conditions for estimating variation in D. D is approximately a 1/avgST like this was attempting.
So detect sudden hash rate changes, I have to loop through the blocks to add up their solvetimes, waiting for a certain X to be exceed so that I have a fixed N expected = X/T and a varying M'. I'll have some level of P required and will know the M' for the unusually slow or fast STs before hand. The M from the loop is converted: M' = M-1 for M>N and M'=M for M<N.
Footnote:
The goal of the difficulty algorithm is to estimate the current hashrate to set the difficulty so that the average solve and confirmation times are as close as possible to the block time, but random enough to prevent orphans.
Assuming we want solve times to follow the exponential distribution it can almost be simplified to "Estimate the current hashrate." That is used to set the difficulty via target = 2^256 / HR / Block_time. But the hashrate depends on the exchange rate, fees, and on the difficulty itself, so the first definition is more complete. We have to use past difficulties to estimate what the hashrate was, but the difficulty we choose affects the hashrate. We could know what difficulty was needed more accurately if we knew the exchange rate and fees, but the difficulty does not have immediate access to fees and no access to exchange rate.
If there is 1 tx/s then average confirmation time is sum(st_i*(st_i+1)/2) / sum(st_i). This comes out to average solvetime if difficulty is always set correctly for the current hashrate, otherwise it is higher. To see a reason why it is true is this: exponential distribution is memoryless, so that a random point in time (a random tx if txs are evenly distributed and sufficiently frequent) will average the average solvetime to the next block (and surprisingly, also average the average solvetime to the previous block, i.e. 2xT between the two sequential blocks because long solvetimes are more common.)
The charts below show the full difficulty history of 5 Monero clones that switched from the Cryptonote default difficulty algorithm (simple moving average with N=720) to LWMA difficulty algorithm.
The fourth plot below at the end is where they switch from Cryptonote default difficulty to Sumokoin's SMA N=17. They immediately had problems because they have a faster solvetime than Sumo and N=17 with Sumo was/is already close to breaking all the time (they haven't switched yet). So they rushed to get LWMA active and were the first to have it. They paved the way for a lot of coins to follow and uploaded a pull request to Monero.

Masari then began to have trouble from on-off mining, even after POW change as shown below.
Here is a close-up. The first plot is the old LWMA that had fewer "blocks stolen". It use average of difficulties instead of harmonic mean. The harmonic mean does not rise as fast in some circumstances and falls faster, so it could be the cause. But the other coins are not having this problem.
These karbo plot are in a more zoomed-in view (fewer blocks per plot) to show SMA with N=17 a lot of oscillations (they started out with Cryptonote default difficulty but then switched to SMA N=17, and now LWMA N=60). The N=17 was really fast, but it caused way too many problems due to varying up and down too much, inviting miners to constantly engage in on-off mining which you can easily see as the oscillations. The new N with LWMA is chosen to be as fast as possible without inviting these on-off attacks with accideintally low difficulty. You can also see a recent timestamp attack due to not having the new timestamp protection (solvetime is 0.68 of the target for that plot which shows they got a lot of blocks much faster than normal (500 blocks in 35 minutes).
This is a repeat of the Karbo data since they began LWMA at 216000. At 3750 blocks per plot, this is on the same time scale of the T=120 coins I show with 7500 blocks per plot, about 10 days per plot.
This describes the a DAG-based blockchain that uses Nakamoto consensus to get permanent ordering in only 1x the propagation delay if there's no increase or shift in network hashrate. Other consensus methods require an exchange of messages which require at least 2x the propagation delay. Tight timestamp limits can prevent <50% selfish mining from disruption the fast consensus.
The following are clock and timestamps requirements in Nakamoto consensus on which my DAG concepts are focused.
To repeat, I'll ignore requirements 3 & 4 for this article.
Most people argue against all of the above requirements based on good intentions that pave a road to attacks on distributed consensus, especially the 1st one. I came up with these after investigating the source of every problem that occurs in difficulty algorithms. It turns out that almost no problems are caused by difficulty algorithms, but by the clock and timestamp rules. I then looked back at Lamport's famous 1978 Clocks paper and thought carefully about how Nakamoto consensus works (e.g. each hash is a "vote") and can firmly claim the above are requirements for distributed consensus. Median of time past is just an ugly patch that reduces the speed of reasonably secure consensus and causes problems in unwary, disparate code.
I'll assume for this article that no one wants to use requirement 4 (RTT) and not discuss it except to say there's no harm in using it as the most recent timestamp in the following algorithms, as long as requirement 3) is applied with sufficiently tight timestamp limits.
[I'm currently working on this article. ]
I'll discuss here everything I know about difficulty algorithms and how they relate to PoW block-based DAGs. In comparing algorithms, "best" or "better" mean the algorithm that has the fastest response speed of response to hashrate changes for a given level of stability when the hashrate is constant. The parameter "N" (or N*M in Digishield) in all of these is 2x the "mean lifetime" of how long it takes the algorithms to respond, so it's a filter on random variation. All of these except BCH's Absolute ASERT require monotonic timestamps to prevent attack, and I'm not sure it's safe (I vetted and approved its use in BCH, with a consensus-theory-based philosophical objection. Our other options at the time would have meant an additional and potentially complicated consensus change, or kyuupichan's timestamp handling in Tom Harding's WT-144 to be implemented in ASERT. It requires going through the previous 11 timestamps (if BTC's MTP ~ 6 is used) and assigning MTP+1 to any timestamp that is before the MTP timestamp before using in the difficulty algorithm).
SMA algorithm
The simplest difficulty algorithm to use in a DAG of blocks is the simple Moving Average (SMA):
Simple Moving Average (SMA) difficulty algorithm
T = desired block time
N = number of ancestor blocks in averaging window
target = 2^256/difficulty in a given block.
target = (2^256/sum_N_ancestor_difficulties) * (most_recent_timestamp - oldest_timestamp) / T
or
difficulty = sum_N_ancestor_difficulties * T / (most_recent_timestamp - oldest_timestamp)
Notice the sum of difficulties is chain work as seen by the block who's target is being cited, which doesn't include siblings etc that the block hasn't seen. The 1st term in parenthesis in the 1st eq can be replaced by average of N target values (this is what Kaspa DAG does based on my recommendations), but more properly, a target-based version would need to multiply each target times its solvetime, sum them up, and divide by N. The "oldest timestamp" makes the same "2015/2016" error that Satoshi made if it's not actually the Nth oldest ancestor's most recent (or average or oldest?) parent's timestamp, or the "most_recent_timestamp" could follow the RTT rule above. All this is not important for large N.
Digishield algorithm
The SMA above can have oscillations if a large percentage of miners come and go based on difficulty changes. A better algorithm to prevent this is Digishield, if you don't include its error of using BTC's forced timespan limits (4x and 1/4 the measured timespan, which allows attacks & slows adjust at genesis) and not use its "MTP delay" in which timestamps it uses (assuming you require monotonic timestamps to prevent attacks from not using an MTP delay) which causes a persistent oscillation. A target version of Digishield is:
Corrected Digishield:
N = 1/M of the N above to have the same stability as the SMA
timespan = Max - Min timestamps which are N+1 blocks apart.
T = targetBlockTime
M = 4 = "filter", "buffer", "tempering", or "dilution" factor. Notice M=1 makes it an SMA.
target = (2^256 / sum_N_ancestor_difficulties) * (1 + timespan/(N*T*M) - 1/M)
Again, avg_N_targets can be used to replace the 1st part in parenthesis. It's presented as a calculation with real numbers which should be allowed so that every validator can agree on the value after the division, so it should be expanded to remove the 2nd parenthesis where integer math division will work with little error.
WTEMA algorithm
A significantly better algorithm ("WTEMA") can simply use a parent's target and solvetime, but I'm not sure which parent to use (oldest, newest, average target and solvetime, one with shortest or longest solvetime, or the one with the highest or smallest target?) and this slightly affects my descendant ordering. Notice how it similar it is to Digishield.
WTEMA difficulty algorithm
N = 2x the N for SMA to have the same level of stability
target = parent_target * (1 + parent_solvetime/(T*N) - 1/N)
Absolute ASERT algorithm
An even better algorithm is BCH's "Absolute ASERT". I prefer the simpler WTEMA but that and a Relative ASERT use only 1 parent target and timestamp and this causes a slight imprecision in how descendant ordering works. They also increasingly (linearly with N) lose accuracy in getting the correct average block time (5% at N=1000?). BCH's absolute ASERT does not have these problems, nor require kyuupichan's timestamp handling if monotonic timestamps are not enforced. It still has the problem of which parent's timestamp to use but it doesn't use a parent's target. This is solved by follow the timestamp consensus requirement number 4 above and use the timestamp in the miner's block to determine his difficulty. BCH's integer-based code needs to be used, but here's the real-valued math.
Absolute ASERT
N = 2x the N for SMA to have the same level of stability
t = time since genesis
h = "height" = number of ancestors, not generations
target = genesis_target * e^((t/T-h)/N)
Propagation delays may change which will affect the minimal-possible confirmation times and it's best and easiest to have a limit on DAG width, if not a fixed width, despite the changes. A way to automatically optimize confirmation time and maintain a certain DAG width is to measure the DAG width and change the desired block time in the difficulty algorithm. Rewards that target a coin emission rate would need to decrease if the block time decreases while the DAG width is constant. Reasoning through the effect of a propagation delay: Delays decreases => DAG width decreases => difficulty per generation decreases if the difficulty algorithm targets a number of ancestors in a given amount of time instead of generations. WTEMA is the only algorithm above that doesn't target either a specific number of blocks or generations per timespan.
[ I'm currently working on this article ]
A DAG for minimizing confirmation times needs to average multiple parents per block (which is also the DAG width). This give tx recipients more "samples of solvetimes" in a shorter time, on the scale of propagation delays, to better estimate how much hashrate support his tx has. If the number of parents per block is not limited this is also the DAG width. The block time multiplied by the DAG width is the propagation delay. But because of the difficulty in "closing out" how old a block can include "previously unseen ancestors" in its history to prevent any significant change in ordering, it may be best to target a small average DAG width of say 2 or 3, especially if we adjust target solvetimes to achieve the desired DAG width which will keep solvetimes a specific fraction (after dividing by targeted DAG width) of propagation delays. A smaller DAG width can also help in reducing the following duplicate tx problem.
A hard problem in a DAG of blocks instead of a DAG of txs is selecting which txs to include in a block. DAGs If a tx propagates faster than blocks, network bandwidth & block space will be wasted on by multiple blocks containing the same tx even if the DAG speed is being fully utilized (i.e. miners empty their mempool in every block they produce). If there's a sizeable mempool allowed to build up, pools can randomly select txs and hope they don't "collide" with other sibling block selections, but that would require a mempool that contains >10x the DAG width to have <10% chance of collision which means txs are slowed by 10x the potential speed before they can get included in a block, eliminating the purpose of a DAG. Pools could agree outside the protocol (or it could be coded if they have a long-lasting destination address for rewards) on which txs they will include based on a hash of each tx in their mempool (to sort them) and also based on each pool's portion of the total hashrate (this can be estimated in the protocol) to determine how many txs they get. This loses some efficiency and reduces the permissiolessness of Nakamoto consensus. A block-based solution is for wallets to "sign transactions over" (in some sense) to a selected pool (maybe wallet owners simply choose a pool to directly send the tx to and the pool does not tell other pools about the tx). The problem might be an argument for each tx being its own block, even letting wallets collect parent txs and mining their own tx.
An idealized network for simple analysis would be N equal-sized pools. An ideal DAG would have a target block time that changes as network propagation delays change so that the DAG width of N stays a constant (N = typical number of parents). the network propagation delay is equal to N*blocktime. I'll assume the descendant ordering method described below is used, which is the most precise & correct order if there are two competing blocks containing a double spend. Descendant work ordering can show a block has 50% of the hashrate support in only 1 propagation delay if the sender of the tx is not adding hashrate to the network to secretly support a double spend. The recipient has good evidence that 50% of the network hashrate has prioritized his tx over a potential (unseen) double spend in N block times (after the tx is included in a block) multiplied by 1.96/sqrt(N) for 95% confidence (the Poisson distribution gets closer to Gaussian with larger N). This is an acceptable wait time for small-valued txs. The minimum time to show there's not a double spend even if the attacker has 49% of the network hashrate is 2*N*1.96/SQRT(2*N) block times. If the recipient sees any double spend in that time period, he has to wait until the txs are too old to be allowed (by the protocol) in new blocks as a "newly-seen ancestor" and then possibly wait a few more blocks for the sum of descendant work to more precisely determine the winner. The "newly-seen ancestor" rule has to be 1x (or 2x?) propagation delays to make confirmation as fast as possible but causes orphans or tip races between 2 competing DAGs. To prevent various timestamp manipulations that can help an attacker, these minimum times to confirmation require honest moners to enforce tight timestamp limits on parent blocks (to allow only reasonable local time error between honest miners, plus propagation delays), accurate local times (no peer or NTP time), monotonic timestamps, and a procedure for properly handling blocks that fall near the timestamp limits (a future article to solve a current timestamp attack that exists in all PoW chains). It also assumes a difficulty algorithm that changes every block (as described below) to help descendant work sort out the winner.
Ordering
We normally think of the earliest blocks as the ones with the least amount of work, but this isn't correct. The winning tips in POW, the ones with txs in blocks when the fork first occurred, are declared "first" by having the most descendant work up until the current time, not the ones with the least ancestor work (otherwise it would let a miner choose by some trickery which tx is first by "virture" of having less hashrate). The following Descendant Work rule is the only method I could think of that would work. In the event of a double spend, the first (aka "oldest") block is the one with the valid txn and it has the most descendant work. You simply add up the difficulties of all his descendants. This can be seen as the basis for ordering when sibling chains in normal POW are orphaned. The "oldest" winning blocks in competing chains in normal POW are not the ones with the least chain work, lowest block number, or earliest valid timestamp because subsequent hashing can void them. The hashes that come after are votes that tell us which blocks were seen first.
TL; DR: The number of hashes that come after a block is how early the block occurred. The scarcity of hashes before the block does not prove it was earlier because fewer hashes has less cost.
The following image shows Phantom/GhostDAG (February 2020 updated paper) ordering in the small circles which is based on ancestor work, which is what everyone (including me) initially assumes. My suggested correction is to use the descendant work shown in magenta. (Note: this is not a correction to how GhostDAG selects blue blocks, but how final ordering should be.) There is some parallel in GhostDAG and descendant work as can be seen by B and F being the "excluded" blocks in GhostaDAG and also having the lowest rank out of their siblings in descendant work. There's no descendant work for JML so they're not ranked, but it's possible to use each blocks' own difficulty as part of the sum of descendant ranking. We should include that difficulty if we know all the txs in the block came before mining on it started. BTC, C comes before D despite both of them having the same number of descendant blocks because C 's descendants had a higher sum of difficulties because they had more ancestors, so even though we're only looking at descendants it's including ancestors, provided the difficulty algorithm is not changing too slowly.
If a tie occurs such as when two blocks have the same ancestors and descendants, an arbitrary rule can decide the winner, like the block with the lowest hash.
footnote [1] There is a common misconception that fast finality is cheaper to attack. If the worldwide hashrate using your POW is not dedicated (non-"rentable") enough to your coin to prevent that, even a slow, big coin like BTC would be subject to double spends, costing only 6x12.5 BTC to get 500 BTC in double spends.
Footnote: How To Do Monotonicity
Only a node's local time, determined independently by each node operator (no previously-agreed-upon oracles like NTP, GPS, or his phone company) should be used because peer time is subject to Sybil attacks. Distributed consensus systems like POW are only as secure as the "truth-without-another-consensus mechanism" of available UTC time.
A miner accepts only parents whose timestamps are < FTL+local_time.
If newest_parent_timestamp >= local_time then temp_local_time = newest_parent_timestamp+1
else temp_local_time = local_time
All code everywhere needs to respect temp_local_time as a constant until local_time exceeds it.
This enforces a strict ordering for the node. It might be called a Lamport Timestamp (see wikipedia.) This enforces a strict ordering on the consensus messages (blocks) being sent and received in the distributed system. This 1978 paper by Lamport seems to say this is necessary for all distributed consensus mechanisms. Here's my forest level interpretation of that paper: Conditions IR2 and IR2' require sequential stamps on messages. Paragraph before conclusion says clocks can't be set backwards for "our situation". In the case of blockchain, this means that clocks can't be set to something before a validated timestamps.
Here "failure" means a delay was over 40 minutes in a T=120 coin. I have not seen a 3 hour delay in an LWMA. Before LWMA, "failure" meant a 3 hour to 3 day delay.
The root cause of these failures is that a large miner (>5x the baseline hashrate) is willing to start mining at a noticeably higher D than dedicated miners are willing to mine at and pushes it up over 30% higher, and then stop. Constant miners leaving when it gets high adds to the oscillations. There does not appear to be any solution. I faster algorithm would reduce the number of blocks he mines from 15 to 20 to about 6, but they can accept the shorter mining time and the faster algorithm can make the delays longer.
I've seen a few days of LWMA failure in 3 coins: Niobio, Iridium, and BTC Candy. These failures revealed LWMA was clearly not rising fast enough. The D-LWMA fixes it's inability to rise fast enough when a > 5x miner jumps on. I have not found a way to help it rise faster when 1x to 4x miners jump on without causing too much instability. Being slow to rise has a purpose: most solvetimes are less than average solvetime. There needs to be some skepticism before rising. This is why LWMA rises the fastest for a given amount of stability. It seems to clearly need to rise faster sometimes, but sometimes that "clarity" is really an illusion: avg of 10 solvetimes < 1/2 the target and avg 5 solvetimes < 1/5 the target each occur on accident more than once per day in T=120 coins.
The LWMA and D-LWMA are awesome at dropping to the correct difficulty in only 1 or 2 blocks. But there is a situation where there is no fix to stopping the long delay. The 3 failures appear to be caused by a 30x miner (30x the "dedicated" miners' hashrate) wanting to begin mining whenever D is < 1/30 the correct difficulty for that miner, and he mines until it rises to 1/15 of the correct D. So when he leaves, there is an average 15x delay which is a 30x delay about 1/4 of the time.
This shows the worst example of LWMA failure that occurred one day in Bitcoin Candy.
Masari data shows a milder version of this:
The bigger peaks average 10xT delays for a single block before the big drops, so this does not qualify as a "failure" as I defined it, but it looks like a situation that can be improved. If the "blocks stolen" does not improve, and if there is a better solution out there, then it is a failure.
Worse, a large percent of your dedicated miners may leave when D rises only 25%. This appeared to be happening in Iridium which had 1 hour delays every 20 blocks where most of the 20 blocks were taken 30x faster by a 30x miner. So the miner had to suffer only a 25% rise in D instead of a 100% rise described in the previous paragraph.
Masari used Sumokoin's algo which is:
next_D=avg(17 D) / (0.8*avg(17 ST) + 0.3*median(17 ST)
ST=solvetimes. The 17 D and ST were 6 blocks behind most recent block. There is a 0.3 instead of 0.2 because the median is ln(2)=0.693 of the mean. Masari claims miners starting taking advantage of effects from including the median. The following shows the 30,000 blocks with this algo. Masari target solvetime was 120 seconds, twice as fast and Sumokoin and Karbowanec .
I will edit this later to show results from Sumokoin with the above algo and Karbowanec with a pure SMA N=17.
See also Tom Harding's RTT paper.
This is a special difficulty algorithm that "tightens the Poisson" of solvetimes, keeping them closer to the target. It continually lowers the difficulty during hashing based on the timestamp the miner assigns while he's changing the nonce.
Update # 5
Here's a post I made about changing reward instead of difficulty.
This TSA type of RTT ("a fast DA inside of a slow DA") may be the only type that is safe for the following reason:
On most DAs (not LWMA for some reason) there is a >51% selfish mining attack where the attacker sets a very far-forwarded timestamp such as 2.7x the averaging window (mean lifetime) of ASERT and then sets each solvetime to zero for about 2.7*mean_lifetime*1.38 blocks. If he has 101% of the network hashrate when he begins (as opposed to being a miner before the attack with 50.5% of the hashrate) then he can submit his blocks in 2.7x amount of time, getting 38% more blocks. BTW, if it's a 50.5% attack described above in parenthesis the attacker may still get get 38% more blocks than he expected, but by leaving the public chain the public difficulty will drop which will invite more hashrate from other sources so that he will not win the chain work race. Getting back to my point, if the ASERT is made an RTT (using current timestamp instead of previous timestamp) this attack can be made much worse because the attacker's 1st block is now very easy instead of as hard as the main chain because he sets the timestamp that dictates his first difficulty.
Update Number 4 (problem with RTTs like the TSA)
This will go into detail about the primary problem with RTTs. With the RTT, there is a risk of orphans from cheaters setting the time exactly on top of the FTL, causing some nodes to reject while others accept. I thought about making the FTL shorter than the max benefit of the RTT (have an RTT that stops decreasing before it reaches the FTL), but it would quickly have the same problem to almost the same degree if the cheaters are > 50% (imagine what happens if there are 3 cheaters in row). I've argued the solution is that cheaters will avoid placing the timestamp "on top of" the FTL for fear of being orphaned. But if > 50% are not dedicated and they see a cheating block past the FTL, they will still mine on top of it because they are likely to not solve it before the FTL and it will help them win a 2-block race block if an honest miner does not mine on top of it. This appears exactly like Emin et al's <50% selfish mining attack where there's impromptu 50% collusion from honest miners merely seeking profit. The best partial solution is to make the RTT not change difficulty very much so that the timestamp cheaters do not have much to gain by risking orphans. But this problem and selfish mining are false problems because honest miners can agree to copy the attacks ("start their own attack") to make the attack lose. For example, if 33% hashrate starts an attack, then 33% of the remaining hashrate can start their own attack, leaving 33% to choose randomly. In this way no one loses or gains. CSW of all people called the honest attack "when gamma goes negative" to which Vitalik (of all people) vehemently complained and berated him with a mic at a conference. So CSW was right where Vitalik was wrong. Emin still considers it a real attack in 2021.
Update Number 3 (the best DA I can think of)
Here's the algorithm I would have all coins use, assuming it is not shown to cause problems. I have not checked to see what small percent adjustment is needed to keep more accurate time.
previousST = how long it took to solve the previous block.
currentST = how long it is taking to solve the current block. It is the timestamp in the
header of this block minus the timestamp of the previous block.
chainTarget = the target that goes into nBits
minersTarget = the target the miner has to solve for this block, based on nBits and the
timestamp in the header.
N=60
chainTarget = previousTarget * (1 + previousST/T/N - 1/N)
N=11
minersTarget = chainTarget * (1 + currentST/T/N - 1/N
nextTarget = minersTarget
Solves taking > 3x600 would be about 5x more rare. There would be fewer orphans from a flatter distribution of solvetimes. The only possible problem I can see is if miners try to forward their timestamps to get lower difficulty That's limited by node validation's FTL requirement, so if everyone competes to do that fairness is retained, so the problem then shifts to the question of the consequences of having a lot of blocks falling on top of the FTL limit, potentially frequently getting temporarily rejected by say half the nodes. The miner risks higher rejection rate for a lower difficulty. This is alleviated by my settings: N=11 allows only a 0.15% drop in difficulty per 10 seconds (with T=600) and I believe you can make the FTL 10 seconds. At the start of the period, difficulty is 6% higher than baseline, giving a strong incentive for the 6x HR increases we're see to not come online to get 10% lower-than-avg difficulty the current SMA allows, because with the above they will be paying 7.5% above avg difficulty for those 1 minute solves. This has a slight incentive problem. It give a > 50% miner more incentive to selfish mine. Instead of paying that extra few percent for fast blocks, he just sets all his timestamps to T in a selfish mine, then finish his last few timestamps fast to make a little more chain work than he expects the public to get. He gets them faster than the public chain so he has to wait and go by to BTC mining. When the public chain's time gets close enough that his last timestamp is not past the FTL, he submits his chain. But he has to be > 50%. The 3% lower difficulty incentive (a 60% HR miner) is not a lot when he has already decided to not selfish mine just to get the 100% blocks instead of settling for 60%.
Here are some modelling results
TSA (A slow normal EMA N=80 with a fast EMA N=11 RTT riding on top)
The negative stolen metric indicates it's costly to try to pick a low difficulty to being mining with a high hashrate. The blue + symbols are the target the miner actually had to solve. The green line is the difficulty that goes on the chain.
Target ST/avgST= 595/599.93 N= 80 and M=11
attack_size: 600 start/start: 130/135
StdDev STs: 1.13
delays: 2.13% stolen: -1.23%

The following shows how the EMA N=11 changes the difficulty depending on the solvetimes.

Update # 2
This article got out of hand in length in complexity, so I'll summarize what a lot of coins could do to have an enormous benefit. Force timestamps to be at least 1 s after previous timestamp, make FTL=10 seconds instead of 2 hours, and revert to node local time 5 seconds instead of 70 minutes. Then apply the following to an existing difficulty algorithm:
T = target solvetime
adjustedT = 0.9*T // this might need to be tweaked for accurate avg T
st = solvetime of current block
st = timestamp in header minus previous timestamp
1/M = fraction you want difficulty harder (target lower) at st = 1 second.
1/10 = 10% harder difficulty at t = 1 s and 10% easier at st = 2*T
target *= (1+st/adustedT/M - 1/M)
For simplicity at a small cost in accuracy to chain work, the target BEFORE this adjustment is the target that goes on the chain.
If preventing chains from getting stuck is the only problem (no coin using LWMA has been stuck) then dropping difficulty exponentially after the solve is delayed will work rather than needing to read this long and complicated article. This algorithm will decreases difficulty by 10% every T=target_solvetime delay. MTP=median of time past = 11 in BTC & ZEC that needs to be changed to 1 to force tight timestamp range (MTP=1 means there will be no out-of-sequence timestamps). The FTL = future time limit is 2 hours in BTC & ZEC and must be reduce to something reasonable like 3xT like all coins that use my difficulty algorithms. This requires changing the "revert to node local time instead of median of peer time" rule from 70 minutes to FTL/2 or your difficulty can be attacked by a 33% Sybil attack on node time.
// This is code to only stop long delays. It is not a symmetrical adjustment like
// the full TSA that has other benefits.
// Deal with out-of sequence timestamps.
// Starting MTP+1 = 12 blocks in past, find the newest timestamp
maxTimestamp = timestamps[-MTP];
for ( i = -MTP+1; i <= 0 ; i++) {
maxTimestamp = max(timestamps[i], maxTimestamp);
}
double solvetime = max(0, minersTimestamp - maxTimestamp);
double T = target_solvetime;
if (solvetime > 6*T+FTL) {
// If you don't like my floating point solution then use e^x = 1+x+x^2/2 & log rules.
double adjust = pow(0.90,(solvetime-6*T-FTL)/T)
// Protect against unlikely event of floating point differences
if( ceil(adjust + 0.01) > ceil(adjust) ) { adjust = ceil(adjust + 0.03); }
else { adjust = ceil(adjust); }
Diff = Diff*static_cast<int64_t>(adjust);
}
Summary
The previous section was only about lowering difficulty if there are long delays. Most of the rest of this article is about making the difficulty adjustment symmetrical.
Benefits:
Drawbacks:
Short summary:
Difficulty is calculated by normal algorithm. It is adjusted based on the timestamp the miner reports. The miner does not know his difficulty until he has selected a timestamp. The difficulty drops approximately linearly as the timestamp gets further from the previous block's timestamp (see chart below). The equation below symmetrically and properly "tightens the Poisson". This gives the correct avg solvetime & prevents excess blocks from being awarded in a selfish mining attack that could otherwise use timestamp manipulation to get more blocks.
TSA equation:
Dout = Din*ST/(T+(ST-T)*e^(ST/T/M) )
where
Din = difficulty from normal algorithm
Dout = difficulty TSA uses
ST = apparent solvetime ((this timestamp minus previous timestamp)
T = target solvetime
M > 1 makes the adjustment more aggressive
Before getting to all the complicated details and code of doing this perfectly, I want to point out the above image shows it can be approximated simply with a linear equation. An arbitrarily-selected linear function may have undesired effects, especially if adjusting reward instead of difficulty. I am only suggesting linear functions that simulate the e^x be used. By using the e^x = 1+x approximation that is darn close for small x, the above difficulty adjustment can be:
M = 5
adjustedT = T*0.893
Dout = Din /(1 + ST/adjustedT/M - 1/M)
Where the 0.893 was determined by modelling constant hashrate to to return the desired solve time T.
To see how this is used more fully:
M = 5;
MTP = 11; // Bitcoin's median time past setting
// Prevent negative solvetimes in a safe way.
// This does not limit timestamps as reported on chain which
// is done by normal future time limit and MTP past limit.
maxTimestamp = timestamps[-MTP];
for ( i = -MTP+1; i <= 0 ; i++) {
maxTimestamp = max(timestamps[i], maxTimestamp);
}
k = 100*T*M; // factor to prevent integer division problem
// The following is an adjustment due to using
// and e^x = 1+x approximation in the adjustment
adjustedT = targetSolvetime*0.893;
// Adjust difficulty that miner has to solve based on the
// timestamp in his block header. Expect miners to push timestamp
// towards FTL to the point of risking their block being
// rejected for too long, after blocks with earlier timestamps
// that will allow blocks after theirs more room assign a later
// timestamp and thereby more easily pull ahead in chain work.
Dout = (D*k)/(k + k*(minerTimestamp - maxTimestamp)/adjustedT/M - k/M);
There is theoretically no difference between increasing the reward and lowering the difficulty.
// Simple TSA method to simulate above image, linearly increasing
// reward (instead of lowering difficulty) from 1/1.3 = 0.77 for
// solvetime = 1 second to 2x for solvetimes > 4x target
SolvetimeRatio = (this_timestamp - previous_timestamp) / TargetSolvetime;
reward = BaseReward / max(0.5, (1.3 - 0.2*SolvetimeRatio);
But make sure out of sequence timestamps are handled correctly as shown above.
Digishield in this context compared to LWMA or SMA
Zcash's Digishield is a good algorithm for KMD that can have > 50,000x hashrate attacks and needs to respond quickly, provided MTP is changed from 11 to 1 and the adjusted difficulty is the one that gets stored as the difficulty for that block on the chain. This is because it only uses the past 17 blocks in averaging whereas LWMA uses 60. Digishield ignores 75% of the effect of the 17 solvetimes to get the same level of stability in normal circumstances. But since the difficulties are being adjusted a lot Digishield will respond ~3x faster. But LWMA will be more stable, so it depends on your needs. This is the only context where Digishield is faster.
How do we handle chain work?
In contradiction to the above section on Digishield, most of the work I've done kept the baseline difficulty on the chain unchanged. In other words the adjusted difficulty is not what's usually stored on the chain or subsequently used in future baseline D calculations. But what should the cumulative difficulty be if I do that? I usually assumed it would be adjusted D, the D the miner solved. But this is not the average D that the miners as a group faced during that block. My future work in this area will make the adjusted difficulty the one used in the baseline difficulty calculation and the chain work. The wide changes in D will be offset by the higher stability in solvetimes. Another option I had not appreciated in the past is that if we change reward instead of difficulty to encourage faster solvetimes (and less reward in the future, the D for the future calculations and chain work is not affected. But a lot of times the amount of mining is not strongly correlated with reward.
This is a day of TSA difficulty on a live coin, exchange. The purple is difficulty, and the lines below it are the average of 11 solvetimes and estimate of hashrate changes based on those times. No other algorithm will have such a wildly varying difficulty and the stability of the solvetimes are similarly unique.

For comparison, here is a typical day of difficulty for Zcash that has a typically-good difficulty algorithm (digishield). The red lines are high-probability instances of sudden increases in hashrate.

Here is a comparison of their average of 11 solvetimes.


[Xchange Code is here.] (https://github.com/Xcgtech/Wallet/blob/abf1b93486e30a4c4877400f2af574f85005a6f8/src/pow.cpp#L47) See comment below for a copy of it with most comments removes
The following chart shows the benefits compared to current methods. "NH" refers to "NiceHash-like" on-off mining that has 2x a coin's baseline hashrate (HR). The curve with a peak assumes NH-like miners will learn how this algorithm works and take advantage of it, making the solvetimes more accurate. The green line is more realistic for most coins because it assumes constant HR. Delays > 4x the target time are equally rare under either assumption, 1 per 43 days instead of 14 times a day for T=120 coins.
See math section below for how the blue and green plots were generated. Histograms are generated by the derivative of the CDF. For example, the Poisson CDF = 1-e^(-t/T). Derivative = 1/T*e^(-t/T). The red plot uses T=1. (BTW, for N samples and bins = n, multiple the derivative by N*n.) A very aggressive setting with M=1 shown below instead of 4 (as above) enforces precise solvetimes even with just constant hashrate, but the difficulty starts out at 20x higher and ends up 10x lower than baseline by 2xT.
Simulation confirmed the math (this is a less-aggressive linear motivation instead of s-curve). Target solvetime on the x-axis was 100 seconds. (5 million blocks)

Results
The following charts compares TSA (with LWMA-1 as its "baseline" algorithm) and LWMA-1 alone. LWMA-1 is the best algorithm I had before TSA for responding quickly to on-off mining. This simulation models the worst attacks I see. They come from using CN8 which attracts NH miners. Notice that TSA does not drop low enough to trigger an "attack" of extra hashrate (3x baseline) as often. The on-off in this model is triggered by the baseline LWMA-1 which is smoother than normal because of TSA, so there are fewer attacks. The solid green bars are the normalized network hashrate. The blue "+" is the actual difficulty the miners have to solve in TSA, based on their timestamp. They can't forward the timestamp because future time limit is made much closer to real time. If they delay the timestamp, D is harder to solve. Notice the oval regions which show there are not any "+" are below average D during the attacks. The attackers are having to pay above average difficulty, maybe 2x higher than the dedicated miners.
Nicehash miners are not going to pay 2x the average difficulty, so the above simulation is not realistic. It was based on them only looking at the baseline D (LWMA1 input to TSA). The following is if they start mining only when actual difficulty they face (TSA) drops below average of past N D's. Notice the blue line at bottom (avg 11 solvetimes) is more stable.
The following is LWMA1 with and without TSA with constant hashrate.
With this model, only 16 blocks out of 1 million were > 4x target solvetime compared to normal stable constant HR coin like BTC that would have 18,000. The histogram looks like TSA M=2 with constant motivation.
Using TSA with other DAs
LWMA-1 is my preferred "baseline" DA for use with TSA, but any other algorithm can be used.
The On/Off Mining Problem
Part of the reason for trying to get consistent solvetimes by adjusting difficulty (D) is to reduce on-off mining that causes subsequent long delays and losses from a higher D incurred by dedicated miners. This is the only reason for spending a lot of time trying to find a fast but smooth difficulty algorithm (DA). On-off mining is only a problem in an environment of >51% "miners" (like NiceHash, ASICs, or Multipools) jumping around to different coins. Otherwise a simple moving average (SMA) DA with N=100 to 200 would be sufficient to track price and longer-term mining trends.
Non-Difficulty Attempts to Prevent On-Off Mining
Coins are trying unique POW and merge mining which potentially reduce >50% attacks which would make on-off mining protection unnecessary. Unique POW seems like an anti-Satoshi idea (almost actively seeking lower hashrate that arguably results in less security against 51% attacks) and will probably fail more and more often in their goals. Coins usually regret merge mining for complex reasons which may be solvable or maybe they should not need solving. In either case, I still see a strong need to deal with existing on-off mining, and I expect the need to increase.
Can we change reward in addition to difficulty?
The idea comes up from time to time of changing reward (R) instead of or in addition to difficulty (D) in order to motivate miners to get more accurate solvetimes. Miners are only interested in the R/D ratio, the higher the better, not R or D alone. In trying to motivate them to start of stop hashing a coin, you can change either by the same percentage and get the same effect. Over the long term a constant or decreasing R per block allows for an increasing D is a lot different than trying to keep a constant D (i.e. hashrate) by varying R, but on a daily basis I can't see that it makes a difference.
Summary of TSA
This is a super fast (current block) difficulty algorithm (DA) to be using in conjunction with existing DAs. The existing DA adjusts for "longer" term trends while the fast DA adjusts for the current miner. It uses only the CURRENT block's solvetime instead of past solvetimes which are used in normal DAs. The miner changes his timestamp to current time as he is hashing and this sets a large change to a baseline D. He has to solve a higher D if he solves it fast, and a lower D if the solve is late in being found. This opens up the potential for timestamp manipulation which is discussed later. In normal DA, we estimate future hashrate (HR) of miners based on PAST hashrates by avg(D)*T/avg(solvetime). In this method, by looking at the CURRENT timestamp and adjusting current D based on it, we are estimating current HR and penalizing that miner and only that miner for high hashrate, not future miners. It makes all solves closer to T which I call "tightening the Poisson". It eliminates long delays in solves.
The equation to to set the fast difficulty (Dout) is based on the standard slow-changing difficulty (Din) and the timestamp the miner sets. T = target solvetime. M=3 to 10ish, the slowness.
Dout = Din*t/(T+(t-T)*e^(t/T/M) )
Here's the plot:

The following is from spreadsheet testing with constant hashrate. The theory is solid: I did not have to make any changes to get nearly perfect average solvetime. The dots are Dout, the fast part of the DA, which is the actual D that miners have to solve. It's based on an EMA N=5. The line is Din, the slow baseline D, from an N=28 EMA.
Code Changes Needed Outside the TSA
Miners / Pool need to change the timestamp in the template while changing the nonce, or pay a higher D than those using current timestamps. At least updating the timestamp once per 5 seconds is probably enough. CN coins do not update timestamps. This must change for TSA to be beneficial.
The validator must use the block's timestamps to calculate the D target that the hash must be below.
If there's an API or template request to get current D, the daemon must calculate it based on it's peer (or system) time.
Reduce Future Time Limit
The FTL (the max time ahead of node time a timestamp can be) needs to be reduced to maybe 1/4 target solvetime or less (30 seconds for T=120) to reduce instances of timestamp manipulators getting lower D at the expense of others. This allows M=5 and M=3 to have max timestamp manipulation of D to be 5% and 10% less. But even if FTL is set too high (like FTL=target), everyone could manipulate timestamps to forward them as much as possible (before some nodes start rejecting their blocks, decreasing chances their chain is built upon) which will increase fairness and effectively prevent the problem. A large miner can only get 1 block "in a row" at low D if he manipulates time better than others.
Reduce allowable peer time difference from system time
A node looks for median of peer time and adjusts its time to be equal the median if it is within a limit, otherwise it uses its own time and might throw a warning. That limit might need to be 1/5 of the FTL to reduce chain splits (6 seconds for FTL = 1/4 of T if T=120). I think nodes and miners should set system time to NTP time (e.g. pool.ntp.org) and constantly throw a warning if median of peer time is not within 5 seconds. NTP methods were supported by Theymos and Mike Hearn. NTP and GPS time could be hijacked in extreme scenarios, but I am not saying nodes have to use NTP time. Time is a knowable fact by all nodes independently without us needing to specify an oracle (NTP, UTC, GPS, Russia's GPS system, a cesium clock, or the stars if your node has the optics for it), so a consensus determination is not needed. Byzantine-tolerant systems such as BTC require clock synchronization. POW and the block chain do not define time, nodes do.
The TSA algorithm: A 1-Block DA
Jacob Eliosoff's EMA gives perfect average solvetimes when using only the previous block's difficulty and timestamp to adjust. It has a perfect symmetry that is based on the Poisson distribution. This makes it ideal for adjusting the D of the current block. It is also a great choice for the baseline DA where you can use the same code with M=30 to be like LWMA N=60. The Din below comes from a normal slow DA (the baseline D). Dout is the output of this fast EMA, the adjustment to Din.
Dout = Din*t/(T+(t-T)*e^(t/T/M) )
I found M=5 to be a good somewhat conservative choice, causing Dout to range 60% to 135% of Din. M=3 would be pretty aggressive. M=10 might have minor benefit. Larger M is a smaller, slower adjustment per block.
See bottom of this page for target code for BTC/Zcash clones
// TSA, Time Stamp Adjustment to Difficulty
// Copyright (c) 2018 Zawy, MIT License.
// See https://github.com/zawy12/difficulty-algorithms/issues/36
// Changes difficulty in current block based on template's timestamp.
// FTL must be lowered to 30 seconds. CN coins / pools must fix their universal timestamp problem.
// CN coins must get pool software jobs & nodes issuing templates to update template timestamp
// to current network time at least once every 10 seconds, not merely setting it to arrival time
// of previous block. Miners outside of pools need to update it without asking for new template.
// Do not change anything below this line. Make the calling code work with this
// so that you do not have errors.
difficulty_type TSA(std::vector<uint64_t> timestamps,
std::vector<uint64_t> cumulative_difficulties, uint64_t T, uint64_t N, uint64_t height,
uint64_t FORK_HEIGHT, uint64_t difficulty_guess, int64_t template_timestamp, int64_t M ) {
uint64_t L(0), next_D, i, this_timestamp(0), previous_timestamp(0), avg_D;
assert(timestamps.size() == cumulative_difficulties.size() && timestamps.size() <= N+1 );
// Hard code D if there are not at least N+1 BLOCKS after fork or genesis
if (height >= FORK_HEIGHT && height <= FORK_HEIGHT + N+1) { return difficulty_guess; }
assert(timestamps.size() == N+1);
previous_timestamp = timestamps[0]-T;
for ( i = 1; i <= N; i++) {
// Safely handle out-of-sequence timestamps
if ( timestamps[i] >= previous_timestamp ) { this_timestamp = timestamps[i]; }
else { this_timestamp = previous_timestamp+1; }
L += i*std::min(6*T ,this_timestamp - previous_timestamp);
previous_timestamp = this_timestamp;
}
avg_D = ( cumulative_difficulties[N] - cumulative_difficulties[0] )/ N;
// Prevent round off error for small D and overflow for large D.
if (avg_D > 2000000*N*N*T) { next_D = (avg_D/(200*L))*(N*(N+1)*T*99); }
else { next_D = (avg_D*N*(N+1)*T*99)/(200*L); }
// LWMA is finished, now use its next_D and previous_timestamp
// to get TSA's next_D. I had to shift from unsigned to signed integers.
// assert( R > static_cast<int64_t>(1));
int64_t ST, j, f, TSA_D = next_D, Ts = T, k = 1E3, TM = Ts*M, exk = k;
if (template_timestamp <= static_cast<int64_t>(previous_timestamp) ) {
template_timestamp = previous_timestamp+1;
}
ST = std::min(template_timestamp - static_cast<int64_t>(previous_timestamp), 6*Ts);
for (i = 1; i <= ST/TM ; i++ ) { exk = (exk*static_cast<int64_t>(2.718*k))/k; }
f = ST % TM;
exk = (exk*(k+(f*(k+(f*(k+(f*k)/(3*TM)))/(2*TM)))/(TM)))/k;
TSA_D = std::max(static_cast<int64_t>(10),(TSA_D*((1000*(k*ST))/(k*Ts+(ST-Ts)*exk)))/1000);
// Make all insignificant digits zero for easy reading.
j = 1000000000;
while (j > 1) {
if ( TSA_D > j*100 ) { TSA_D = ((TSA_D+j/2)/j)*j; break; }
else { j /= 10; }
}
if ( M == 1) { TSA_D = (TSA_D*85)/100; }
else if (M == 2) { TSA_D = (TSA_D*95)/100; }
else if (M == 3) { TSA_D = (TSA_D*99)/100; }
return static_cast<uint64_t>(TSA_D);
}
Choosing baseline DA to get Din
Just use any decent algorithm that's relatively slow such as the following 100-block SMA. But TSA needs
out-of-sequence timestamps to be handled as in the code above when it is determining the time since previous block.
// CD = cumulative difficulty, TS = timestamps, H=height
Din = ( CD[H] - CD[H-100] ) * T / ( TS[H]-TS[H-100] );
The denominator should have a divide by zero protection like std::max(1+T/50,( TS[H]-TS[H-100] ));to prevent a 100-block selfish mine with all the same timestamps causing a divide by zero error on the block after he submits his chain.
Getting the individual solvetimes
Use the method above for safely handling out of sequence timestamps. Do not do the following because a reverse time stamp can be sent, and be truncated, but the next timestamp will have a large value from the subtraction which will lower difficulty.
if ( t < 0) { t=0; } // DO NOT DO THIS
CN pools
I am told CN coin pool software do not allow miners to use accurate timestamps. Miners must use the previous block's arrival time which they are assigned in the template by the pool. The easiest solution is to modify the pool software to keep the correct timestamp and miners make a new request for the template every so often, but the request makes miners lose some time. So a balance needs to be between this wasted time and not getting the lowest D possible. For T=120 with M=2 and M=4, D drops about 5.5% and 2.4% every 10 seconds. Turning this into an equation, my estimate for how often to update timestamps is
update_timestamp_seconds = SQRT( template_delay * T * M / 1.8)
For example if it takes 0.2 seconds to get template and restart hashing and T=120 and M=5, then it's once every 8 seconds. This is trying to make the % decrease in D while waiting on an update = % hash time lost to getting the template. My estimate of % D drop in 8 seconds from this is 0.2/8 = 2.5%.
Possible Risks
Tightening the Poisson increases the risk of blocks being found at the same time which will increase chain splits. Miners can set an old timestamp after a block has been found to get a higher difficulty and thereby create an alternate chain with more work, but their profit and risks seem no different than block withholding profit and risks (if < 50% hashrate). They can do the opposite and assign a forward stamp to get lower difficulty, but they risk too many nodes not accepting if they get too close to the FTL. Another block will need to be added before the node looks at it again and thereby let it pass the FTL test, so it's not definitely excluded forever. But such a cheat risks other blocks with higher D being found. I believe setting an FTL as small as possible (expecting maybe 10% of nodes to reject blocks with good timestamps) is the best course because cheaters will trying to forward the time close to FTL to get lower D which will make the next block have higher D. Miners can then fine-tune their clocks forward or reverse for maximum profit at the expense of others not fine-tuning. This is a small penalty compared to letting a huge amount of hashrate jump on and get several blocks in a row. They can't get more than 1 block at a cheaper difficulty.
Timestamp manipulating and more alt chains should be expected, but the existing chain work methods seem like they can easily provide sufficient protection.
Background on Node Peer Time
I have not been able to find an argument against letting the nodes be more restrictive in the FTL they allow miners. Pre-PBFT Byzantine-tolerant systems required a synchronization clock, and PBFT can be asynchronous, so it seems theoretically acceptable that nodes can ultimately define a tight max forward time (and not just to prevent miners colluding to lower difficulty by accelerating time). In other words, the "timestamp server" function of miners is to make blocks sequential, not necessarily or even feasibly responsible for respecting real time which apparently can be left up to the nodes. Node peer time seems to be a feeble consensus mechansim, but has worked despite what a Sybil attack could do. Nodes' time could be backed by NTP or not, or use only an oracle like NTP, or just let every node independently determine time (my and kjj's preference). See this old interesting discussion between kjj, theymos, and Mike Hearn.)
The peak in the first plot above needs some explaining. I could choose other reasonable functions such as constant hashrate h=1 which is the green-line plot. A simpler linear function gave a very similar curve to this more realistic S-curve (it models more accurately the on-off mining that occurs in response to changing values of D). Units clarification: H and h in the following are hashes per second. D is hashes per block and T is seconds per block. For BTC clones difficulty = D * 2^n where n depends on the "maxTarget" or "powLimit" of the coin (n is the number of "leading zeros in the max target). D = (2^256-1)/(nBits as a target).
Update: In the following I state H = hashes/second, but H = hashes. The math below uses slight of hand to cover up that error.

The green-line plot assumed the simpler assumption that hash rate will be constant during the block, i.e. h=1.
The following was the previous leading text of this article, before I realized the perfect version of Andrew's idea is just another difficulty algorithm being applied to a single block.
Andrew's Sexy Long Tail (Idea)
This purpose for this issue is to explore an idea by Andrew Stone. See also here. He understands there is a large amount of futility in trying to do a DA that is any better than a SMA. So he came up with this sort of bold idea that thinks and goes outside the box. In order to prevent long solvetimes, he suggests decreasing difficulty DURING the block, based on when the block is finally solved. That is, based on the timestamp selected by the miner's pre-hash template-creating software. So if there's a delay in a block solve, the D gets easier so that miners have more motivation to start mining. Alternatively, reward could be increased but is no different from a miner's point of view as explained above. Either method requires some consideration in the DA in order for the coin emission rate to stay on track.
Difficulty for the block is determine by applying an adjustment to the "initial" D of the block, given by the standard DA, if the timestamp is past some limit that is longer than we think is desirable, possibly without trying to modify the Poisson distribution, such as only making a change if the solve is taking >5x the target solvetime T ( >5xT occurs in 4% of the blocks if hashrate is constant).
Consequences & Considerations
Miners can choose their timestamp up to the future time limit (FTL) and back to the median of the past 11 timestamps (MTP). To get lower difficulty in this scheme, they will try to select a time as close to the FTL as possible while trying not to have too many nodes reject their block. If they send blocks to a node with an FTL further in the future than other nodes, their solves will be sort of hidden (rejected) by the rest of the chain until that time passes. Nodes might follow a rule that if a node is sending blocks with > 2*FTL stamps, it gets banned. Since all miners might try to forward stamps, the FTL probably needs to be pretty "tight". It seems like FTL = T would work. Since miners with custom software will be able to forward timestamps, all miners should be provided with software that allows them to select timestamps, or a good default selection be used. But this later option is no different than lowering the FTL. Since a smart miner knowing the trade-offs better than others will be able to select the optimal timestamps to his advantage, the incentives provided by this should be conservative. For example since > 6xT solves are rare, if we have FTL = T, then maybe the rule should not decrease D until after 7xT, at which point we are going to let those smart miners get their gain, and other miners will not miss out much. The incentive would not be extreme because NiceHash could send D higher with a sequence of fast solves (and thereby cause subsequent long solves) while it goes to mine other coins, then come back at the right moment to get low D. This brings up the question of if the short solves should cost more D which I'll call symmetrical incentive and address it further below.
If miners lower their D by a forwarded timestamp, they risk losing the largest-chain-work battle to an honest timestamp. This may or may not offset some of the desire to forward timestamps.
Specific Long Tail Example
Usually a 33% decrease in D is enough to bring in maybe 3x more hashrate (HR). Solvetimes more than 5x the target solvetime (T) occur only 4% of the time. So if I were to implement Andrew's idea, it would be to start lowering D linearly from D to maybe 0.66*D (not lower) from 5xT to 8xT. If it takes more than a 33% drop, there are bigger issues that this should not try to address any further. This is a decrease of 11% per T from 5xT to 8xT. So the difficulty algorithm would begin with a normally-calculated D received from the a standard difficulty algorithm such as simple moving average and be adjusted by the template-generating routine to
if ( t > 5*T) {
Dout = Din*(1 - 0.11*(t-5*T)) ;
Dout = std::max(0.66*Din, Dout);
} else { Dout=Din; }
where t solvetime of the block. See section near bottom of how to carefully get this value.
What D should be used for the adjusted-D blocks in the DA's averaging? Any estimate will probably work out OK unless there is a serious problem with a lot of delays and/or the estimate is bad. The initial D is too high and the final D is too low. A simple average of the two is wrong, but it may be close enough. Treating them as two different blocks and pretending the high D was solved in the 5*T cut-off time is too high because it was not solved, but that should be OK. Maybe the high D and the 5*T time it took to "not find it" can be removed from the averaging and we use just the average of the Dout which would be (Din+Dout)/2 and the solvetime would be t-5*T. But a max 30% difference in the D in a 60-block window is not going to make much difference, however it's done, as long as there are not a lot of delays. The estimate should not overshoot the next D calculation or there could be a feedback that causes more delays ... that causes more delays. Dout can be obtained from the cumulative D and Din can be obtained from back-calculating it by the solvetime.
Making it Precise & Symmetrical
I mentioned to Andrew in the BCH mail list the possibility that making the motivation "symmetrical" was better and he was open to it, By this I mean higher D for faster solvetimes in addition to the lower D for long solvetimes (STs). To do this correctly it seems the change in D should be proportional to the normal probability of finding a block. By this i mean we probably do not want to change the general shape of the Possion, except to make it "tighter" i.e. more narrow in width near the target solvetime (T). We want a motivation that "follows the Poisson". To do this we have to use the Jacob Eliosoff's EMA as a basis for the adjustment.
I have not fully tested this like the CN version above but Kalkan of Xchange (XCG) did and found that the solvetime avg was low. This may have to do with averaging targets instead of difficulties in the pre-TSA (LWMA) part. Instead of LWMA, a simple moving average difficulty algorithm will probably correct it. I may or may not work to fix and test it later. The 2nd-to-last line by Kalkan is a patch that should reduce the error in whatever pre-TSA difficulty algorithm is used.
// Start with existing difficulty algorithm, then do TSA:
// LWMA difficulty algorithm
// LWMA Copyright (c) 2017-2018 The Bitcoin Gold developers (h4x4rotab)
// LWMA idea by Zawy, a modification to Tom Harding's wt-144
// Specific LWMA updated by iamstenman (MicroBitcoin)
// Recommend N=120. Requires Future Time Limit to be set to 30 instead of 7200
// See FTL instructions here:
// https://github.com/zawy12/difficulty-algorithms/issues/3#issuecomment-442129791
unsigned int LWMA_TSA(const CBlockIndex* pindexLast, const Consensus::Params& params,
int64_t templateTimestamp) {
// Begin LWMA
const int64_t T = params.nPowTargetSpacing;
const int64_t N = params.lwmaAveragingWindow;
const int64_t k = N * (N + 1) * T / 2;
const int64_t height = pindexLast->nHeight;
const arith_uint256 powLimit = UintToArith256(params.powLimit);
// For startup:
int64_t hashrateGuess = 1000; // hashes per second expected at startup
arith_uint256 targetGuess = 115E75/(hashrateGuess*T); // 115E75 =~ pow(2,256)
if ( targetGuess > powLimit ) { targetGuess=powLimit; }
if (height <= N+1) { return targetGuess.GetCompact(); }
arith_uint256 sumTarget, nextTarget;
int64_t thisTimestamp, previousTimestamp;
int64_t t = 0, j = 0;
const CBlockIndex* blockPreviousTimestamp = pindexLast->GetAncestor(height - N);
previousTimestamp = blockPreviousTimestamp->GetBlockTime();
// Loop through N most recent blocks.
for (int64_t i = height - N + 1; i <= height; i++) {
const CBlockIndex* block = pindexLast->GetAncestor(i);
// Out-of-sequence timestamp protection idea inherited from kyuupichan
thisTimestamp = (block->GetBlockTime() > previousTimestamp) ? block->GetBlockTime() : previousTimestamp + 1;
int64_t solvetime = std::min(6 * T, thisTimestamp - previousTimestamp);
previousTimestamp = thisTimestamp;
j++;
t += solvetime * j; // Weighted solvetime sum.
arith_uint256 target;
target.SetCompact(block->nBits);
sumTarget += target / (k * N);
}
nextTarget = t * sumTarget;
// The above completes the BTG/MicroBitcoin/Zawy code except last 3 lines were removed.
// Now begin TSA.
// TSA Copyright (c) 2018 Zawy, MIT License
// First implemented w/ modifications on live coin by Kalkan of Xchange
// R is the "softness" of the per-block TSA adjustment to the DA. R<6 is aggressive.
int64_t R = 4, m = 1E6 ST, i, f, exm = m;
if (templateTimestamp <= previousTimestamp) { templateTimestamp = previousTimestamp+1;}
ST = std::min(templateTimestamp - previousTimestamp, 6*T);
// It might be good to turn this e^x equation into a look-up table;
for ( i = 1; i <= ST/(T*R) ; i++ ) { exm = (exm*static_cast<int64_t>(2.718*m))/m; }
f = ST % (T*R);
exm = (exm*(m+(f*(m+(f*(m+(f*(m+(f*m)/(4*T*R)))/(3*T*R)))/(2*T*R)))/(T*R)))/m;
arith_uint256 TSATarget;
// 1000 below is to prevent overflow on testnet
TSATarget = (nextTarget*((1000*(m*T+(ST-T)*exm))/(m*ST)))/1000;
// Next line is by kalkan of Xchange to fix low-solvetime problem. May cause overflow on testnet
// A better pre-TSA algo than LWMA above will prevent the need for this.
TSATarget *= (T*k)/t;
if (TSATarget > powLimit) { TSATarget = powLimit; }
return TSATarget.GetCompact();
This discusses the start-up and MTP delay problems in Digishield (e.g. Zcash). It works good, but it has two problems that arguably make it not a lot better than an SMA with N=75. "Better" means that for a given level of stability during constant hashrate, it responds faster to sudden increases in hashrate. With MTP and 16%/32% removed, and safe timestamp handling in place, it easily beats SMAs. With N=17 and a tempering factor of 4x in the normal Digishield, an SMA with N=17x4=68 has the same stabilit but slower response.
There is a +16% to -32% "nPowMaxAdjust" in Digishield v3 that caused me to screw up Bitcoin Gold's new difficulty algorithm as I reported here and here. They were going to use Zcash's Digishield v3 code directly, but I recommended a switching to a Simple Moving Average (SMA) with N=30 to let it respond faster. By making it respond faster, a big problem with the +16% / 32% limits was exposed. Further investigation revealed the limits do not help Digishield in any way and double the number of blocks it takes Digishield to reach the correct difficulty after startup from 260 to 500.
If previous difficulty is accidentally low, a hash attack is motivated. If the accidentally low difficulty (which will occur often in faster-responding difficulty algorithms) is lower than average D by more than the 16% limit, then difficulty is limited to increase to the 16% for 1 block, but then it can't rise very fast anymore because the limit is based on the avg D, not the previous D. The 16% limit (which is a actually 19% limit when expressed as 1/(1-0.16)) frequently placed a 0.5% to 1.5% change per block in BTG's previous SMA N=30 algorithm, which I expected to be 2x faster. But as a result of the limit, it was 5x slower. Digishield isn't experiencing a problem because the trigger is never activated. The limits are [sarcastically speaking] good code as long as they are never used.
No timespan limits should be used in difficulty algorithms because it opens up a catastrophic attack I discovered and detail in my timestamp attacks article. Most coins are affected, including BTC, LTC, Dash, and BCH. The attack results in unlimited number of blocks in 3x the difficulty window, but requires enough hashpower to perform a 51% selfish mining attack.
The following is what was intended and should have been coded more directly. If this had been the code, there would not have been any problem. The difference is that the "correct" code below limits the per-block change in difficulty (as I assume everyone expects the limits to mean) instead of limiting the timespan changes, which unexpectedly makes a big difference. Limiting timespan limits the average of the past difficulties, not the previous difficulty. Limiting timespan was inherited from the 4x and 1/4 limits in BTC, but in BTC a limit on timespan is a limit on previous difficulty & avergae of past difficulty because the difficulty is not changing every block.
if (next_D > previous_D/(1-0.16) ) next_D = previous_D/(1-0.16);
if (next_D < previous_D/1.32 ) next_D = previous_D/1.32;
The following compares BTG's actual difficulty to what it would have been if it was a simple SMA with N=30 (as I was expecting). The semi-straight lines are where the limits are being hit. Notice they start out flat (horizontal) where only 0.5% rise per block was being allowed when we desperately needed the full 16% to be allowed. The green peaks would not have gone so high if it were the difficulty.
It causes a problem at startup: Digishield coins take 500 or more blocks to get to the correct difficulty, literally giving them away. This giveaway causes the difficulty to then overshoot, causing delays while it gets back down to the correct level. In the Zcash example below you can see it did not overshoot which is because they had a slow start period where the reward was really small. They did the slow start at least in because they were warned by another coin that difficulty would cause a problem at start up.
To prevent the problem delete all the following code:
nPowMaxAdjustUp = 16;
nPowMaxAdjustDown = 32;
int64_t MinActualTimespan() const { return (AveragingWindowTimespan() *
(100 - nPowMaxAdjustUp )) / 100; }
int64_t MaxActualTimespan() const { return (AveragingWindowTimespan() *
(100 + nPowMaxAdjustDown)) / 100; }
if (nActualTimespan < params.MinActualTimespan())
nActualTimespan = params.MinActualTimespan();
if (nActualTimespan > params.MaxActualTimespan())
nActualTimespan = params.MaxActualTimespan();
The 16% / 32% limits are only 1/2 the cause of the startup problem. Even without the limits, the 4x "tempering" in Digishield causes 260 block delays at startup where SMA and LWMA cause 140 and 60 block delays respectively, as shown in the image below which shows a 1000x increase in hashrate for 400 blocks (all the red). Interestingly, these delays are the same for any > 50x hashrate increase.
Most Digishield v3 implementations do not get data from the most recent blocks, but begin the averaging at the MTP, which is typically 6 blocks in the past. This is ostensibly done to prevent timestamp manipulation of the difficulty. However, there are several different methods of dealing with bad timestamps that will not inject this delay.
These charts show hashrate jumps on Digishield coins when difficulty accidentally falls low. But I think there is a distinct excess of oscillations that is being caused by the MTP delay.
The lack of symmetry (+16 / -32 instead of +16 / -16 limits) has made things worse for Bitcoin Gold. BCH EDA also had a lack of symmetry where it could rise faster than fall which led to oscillations and too many blocks being issued. BTG also has the ugly oscillations and 3% too many blocks are being issued. The oscillations are obvious, but are not causing terrible delays. Although the 16/32 limits are not close to what's needed and meant by "asymmetry", at least the avg solvetime would have been correct if they were symmetrical, if not fewer oscillations.
The Digishield v3 code has tempering that only seem to be only slightly better than using SMA with N=68.
nActualTimespan = params.AveragingWindowTimespan() + (nActualTimespan -
params.AveragingWindowTimespan())/4;
Simplifying the math this is:
nActualTimespan = 0.75*params.AveragingWindowTimespan() + 0.25*ActualTimespan
The params.AveragingWindowTimespan() is just a constant N*TargetSolvetime. This equation takes only recent data into account, but it includes some skepticism about changing from the past.
Digishield v3 code is effectively:
# Digishield v3 difficulty algorithm
N=17
# ST = solvetime
T=<Target Solvetime>
# Step 1: Insert a harmful delay in your difficulty's response.
sumST = [last - first timestamp, N blocks apart, delayed 6 blocks) ]
# Step 2: Do tempering that actually helps
sumST = [ 0.75*T*N + 0.25*sumST ]
# Step 3: Insert a POW limit to do the exact opposite of what you want.
sumST = (1 - 0.16)*T*N if sumST < (1-0.16)*T*N
# Step 4: Make it asymmetrical so that if your POW limits are utilized, it will cause
# oscillations and make your average solvetime too low.
sumST = 1.32*T*N if sumST > 1.32*T*N # disastrous asymmetry waiting to happen
next_D = sum(past N D's) * T / sumST
Once the bad stuff is removed, the resulting Tempered SMA works better than an SMA with N=65.
This issue has been closed because of prior errors and the issue after this one replaces this article.
This link explains why ETH's difficulty algorithm is the way it is:
https://github.com/ethereum/EIPs/blob/master/EIPS/eip-2.md
In particular, they did not want the difficulty to precisely change with timestamp or miners would start (and did start) assigning lowest timestamp to get higher work. By lumping solvetimes into larger groups that have the same effect on difficulty, manipulation is reduced but not prevented. It stops the biggest problem which was all miners assigning a +1 second timestamp. Part of the problem is that it's looking at current solvetime instead of previous solvetime. That has good and bad effects as discussed in my TSA article. The bigger problem seems to be that the solvetime is too fast.
Ethereum's difficulty algorithm without the difficulty bomb is:
diff = parent_diff + parent_diff / 2048 *
max(1 - (block_timestamp - parent_timestamp) // 10, -99)
A stack exchange answer explains the above. See also my article on ETH's DA for a more detailed exploration.
If the integer division that makes fast solvetimes = 0 and if max is not used it is:
diff = parent_diff * (1 + 1/2048 - 1/10/2048 )
This is the same as the simplified EMA:
diff = parent_diff + parent_diff/N - parent_diff*t/T/N
where
t = parent solvetime
T = target solvetime
N = extinction coefficient aka "mean lifetime" aka number of block to "temper" or "buffer" the size of the response. It can't be too small or a negative difficulty can result from long solvetimes.
This is very close to the theoretically best algorithm which is an exponential moving average (EMA) that I and others have investigated. It's an approximation of the EMA by the taylor series expansion of the exponential function:
e^x = 1 + x + x^2/2! + ...
Where you use the approximation e^x = 1 + x in the EMA algorithm:
diff = parent_diff*( 1 - A + A*T/t )
where
A = alpha = 1-e^(-t/T/N)
See #17
This algorithm was discovered by Jacob Eliosoff who was already very familiar with EMA's for stock prices. He needed to modify it to fit difficulty, and the result turns out to be a known version that's mentioned in Wikipedia in regards to estimating computer performance:
https://en.wikipedia.org/wiki/Moving_average#Application_to_measuring_computer_performance
I say it's theoretically best because you can reduce N all the way down to "1" and the mean and median solvetimes are close to the expected T and ln(2)*T. So it's the best estimator (I know of) of guessing the current hashrate based on only the previous block.
In practice, miner motivation and the way the LWMA responds makes the LWMA a little bit better algorithm. And the EMA can't be used for Cryptonote coins because the timestamps are at the beginning of the block solve, not when the block was found, so there is a 1-block delay that causes substantial oscillations, especially if N is less than 100 in order to be reasonably fast.
ETH's DA has an average solvetime of 14.6 seconds, so to compare it to EMA, I use T=15.
Has anyone used difficulty to get constant-dollar developer or node fees? Difficulty is exactly proportional to network hashrate, and network hashrate is closely proportional to coin price.
Say a coin is currently $1.23 and someone wants to get a fixed income from the coin like $0.01 each time something occurs. To achieve this they could use a constant that is multiplied by the difficulty:
fee = 0.0123 / difficulty_at_$1.23_per_coin * current_difficulty * reward_at_$1.23 / current_reward =~ $0.01
Dollar value here is constant-value relative to when the ratio was determined (when difficulty was at $1.23). If hash power is not able to keep up with coin price (which is a temporary effect), the value would be larger than expected. Otherwise, the real-world value slowly decreases as hashing efficiency increases, which may be a desired effect if it is for dev fees because software gets outdated. But Moore's law has gotten very slow for computers. Hashing should get closer to being a constant hardware cost per hash.
Also, electricity is more than half the current cost of hashing and could soon be 3/4 or more of the cost. Worldwide electricity cost is very stable and possibly the best single-commodity measure of constant value.
The metric might be useful only when the coin is being used as payment, but any long-term contract needing constant value (such as employee/employer contract for salary) could get paid in an inflationary currency or in any other cryptocurrency that has an exchange with the coin. Neither employer nor employee need to use the coin or the exchange because the amount paid (as specified in the contract) would just depend on the initial ratio and current difficulty. The employer would need to argue for a higher ratio and the employee would need to consider if the future price/difficulty ratio might decrease.
The metric is not as good as basing contracts on an index of world-wide electricity cost, so it would mainly be used if payment needs to be in that coin. It connects the coin to the outside world, without depending on a 3rd party like an electricity index.
The following is a difficulty algorithm who's window is based on a time instead of blocks. I have not tested it and it probably has a symmetry problem that will make the avg solvetime too low or too high, if not cause oscillations, or worse. It has strong protection against bad timestamps not only because of the 30 and allowing negative solvetimes.
Nmax=100
# Set the amount of time that has to pass before calculating next difficulty
# We're doing a 100 block SMA unless solvetimes are < target
TT = Nmax*TargetSolveTime
Nmin =30 # lower would be good, but need more protection against bad timestamps
N=0
for (i=-1 ; i=-Nmax ; i--) {
sumD+=D[i] # sum difficulties
N++
sumST = median(T[-1],T[-2],T[-3]) - median(T[i],T[i-1],T[-2]))
if (i < -Nmin AND sumST > TT ) { last i }
}
FINISH
<Do SMA, Digishield, or WHM algorithm with this N>
Here are all the common difficulty algorithms. All equations are expressed as floating point to make the math clear. Typically, you expand the equations for target's really high value to reduce the error caused by integer division. Floating point is never supposed to be used in financial applications or applications that require every validator to get the exact same value.
Limits on timespans, timestamps, and target changes are not included because they enable attacks
Some algorithms place a limit on how much timespans, timestamps, and/or target can change per block. I haven't included any of those limits because they always allow exploits on the consensus. This is because the limits change the math which is supposed to provide a fair estimate of hashrate. The estimate determines the difficulty and the sum of difficulties (i.e. chain work) determines consensus, so the limits are corrupt the consensus mechanism by preventing the math from providing a fair estimate of hashrate. I've described the 15 different exploits in detail in Timestamp Attacks. An example is the 4x and 1/4 timespan limits in BTC that, in combination with allowing out of order timestamps, allows unlimited blocks in finite time. I'm not referring to BTC's "2015" error aka Zeitgeist aka GeistGeld attack described long ago by Artforz. But there's a limit that's always required: requiring sequential ("monotonic") timestamps is a fundamental requirement of distributed consensus which Lamport derived in 1978. Nakamoto consensus does not get around his derivation which didn't assume any class of algorithms. It only assumed distributed consensus is the goal. This 1978 paper might be 1/4 the reason he got the Turing award. Several BIPs have had to deal with the problems caused by violating this requirement. The BIP patches (such as median of past 11 timestamps) enforce the monotonicity rule in roundabout ways.
A Long Sidebar on Real-Time-Targeting
All the algorithms can be made theoretically more accurate by converting to an "RTT" (Real Time Target) by making the most recent timestamp in the equations tN+1 instead of tN. This means making the difficulty of a block depends on the timestamp the miner assigns to that self-same block. This "timestamp-manipulatable-difficulty" is the problem everyone has with RTTs, but it's not a problem if honest miners keep and enforce accurate timestamps which is a separate article I need to publish that shows how to also stop selfish mining. In short, honest miners ignore a block for 2 block times if the timestamp is more than a few seconds into the future.
Tom Harding developed an RTT and implemented Chain2 as a reference implementation that targets an accurate solvetime for each block. I didn't include in the list but it is target = prior_target * C * (t/T)^k where C is a constant and k>=1 and a larger k means a tighter distribution of solvetimes around T. "t" in this equation is different from the others. It's the miner's timestamp minus the timestamp of the previous block, not the solvetime of the prior block.
TSA is the only algorithm shown below that is exclusively meant to be an RTT. It is a fast-responding ASERT inside of a normal slow ASERT. To use it, the ASERT value will be the "official" difficulty for the block that is used to calculate chain work and to be the target used for the next block's ASERT calculation. The sub_target is the "actual" difficulty the miner has to solve for the block. It depends on the timestamp the miner assigns to the same block. P in TSA is a value less than M that causes the difficulty to be higher than the ASERT value if the solvetime is too fast, and lower if the solvetime has been taking too long. The TSA can be similarly done in terms of a fast EMA inside a slow EMA (or an LWMA). See TSA article for more detail such as how to handle timestamp manipulation. I helped JL777 implement an RTT like this on steroids for Komodo because some of their small sub chains were getting 1,000,000x increase & decreases in hashrate. It stopped attackers from getting more than 2 blocks cheaply and prevented stuck chains when they left.
Determining the Best Algorithm
ASERT appears to be the only (nearly) perfectly correct difficulty algorithm. See bottom for a full discussion. WTEMA is much simpler and almost exactly equal to it.
ASERT appears to be the best DA in terms of theory and practice. The "relative" form has more error than the "absolute" ASERT due to nBits having up to 2^(-15) error that accumulates linearly with N (a 1% increase in average solvetime for each 330 increase in N if nBits is staying in that "highest rounding error" range). There can also be a "linear with N" error in the e^x calculation because it must be done with integer math and validators have to calculate the exact same value (floating point isn't supposed to be trusted to be accurate on different systems for any consensus or financial application). Any consistent errors can be "fixed" by changing T in the equations. The errors are small for reasonable values of N (N>500 would be an unusually slow adjustment or a DAG). See BCH's ASERT for the code to implement absolute ASERT. I prefer EMA which has the same errors as relative ASERT but it's a lot simpler to code and is the same except for a small e^x = 1+x approximation error. LWMA is about the same as these and does not have their problem of a >50% attack that can get 38% more blocks in a given time period. All the other algorithms should be avoided. An RTT algorithm could be used to give a more even spread of solvetimes and it can be shown to be the best on every metric, but doing it safely is complicated and no one believes me that it's possible to do it safely.
Testing ranks the ability of the algorithms from best to worst like this:
The method of testing first puts them on equal terms by adjusting their primary parameter to have the same Std Dev in difficulty during constant hashrate. This turns out to be the following for the N and M parameters in the equations:
Once the "averaging window" parameter N is selected to give the same level of stability under constant hashrate, I compare them during on-off mining "attack" conditions. I look at how well they prevent attackers from getting lower targets per hash (using time-weighted target averaging) compared to "dedicated" miners (Mark Lundeberg suggested this) and how well the DAs prevent long delays to confirmation. Jonathan Toomin showed me this is not simply how long it takes blocks to solve, but requires pretending there is (for example) 1 txn every second and do the averaging for that. For a given solvetime st, the total waiting time for all the 1 tx/s confirmations for that block is st*(st+1)/2. You sum this over many blocks and divide by the sum of st's (because it is equal to the number of txs at 1 tx/s) which gives a more correct result for delays than averaging the average wait time (averaging st/2 values). Under constant hashrate with a good DA the average wait time is equal to the average average solvetime**, but on-off mining changes the Poisson distribution causing average delays to be higher than average solvetime, and an ideal DA keeps it as low as possible.
** The average wait time for a tx is not 1/2 the average solvetime even in the case of constant hashrate because some blocks come really slow which offsets the lack of delays in the fast solvetimes. The mean time to find a solution for random points in time (like when someone chooses to send a tx) is 1 block time (not 1/2 the block time aka long-term average solvetime) because "a Poisson process has no memory", i.e. long wait times biased the mean higher than you would expect.
Selecting the Averaging Window Size
As important as the selecting the difficulty algorithm is selecting the averaging window size. I have historically chosen averaging windows that were too fast due to not having the right metrics in testing and due to seeing all Monero clones blow up from oscillations which I mistakenly thought was due to the long 24 hour averaging period in their SMA, but it was mostly caused by its delay, cut, and lag parameters which were good intentions gone really bad. SMA allows oscillations to continue but delay, cut, and lag (esp delay) force oscillations. As a result, most of the 60 or so coins using my LWMA have N=60 and the few using N=90 to N=144 are performing better. I can't find an error in Jonathan Toomim's work for BCH that indicates N=288 for ASERT/EMA is best (which is like N=576 for LWMA) and this is with T=600. With lower T's like the LWMA coins usually have, even a higher N might be best. BTG has been using LWMA N=45 and it's been one of the best & safest algorithms out there. I've recommended they go to at least N=90 while the raw "science" is saying 576. LWMA N=576 will take 2.5 days with T=600 to fully respond to a 20% increase in hashrate (which might be caused by price change). I prefer 1/2 or even less of what Jonathan's work is showing as best because it's more in my realm of experience and I'm afraid of a coin getting stuck. This gives me ASERT/EMA with M=144 and LWMA/WT with N=288 is probably best in all coins. Coins seeing large daily changes in price or on-off miners who often drive the difficulty a lot higher than makes sense might be better off with 1/2 these values.
Algos in terms of difficulty
I chose to express the equations in terms of targets instead of their inverted forms that use difficulty. The inverted forms of these equation (that use difficulty as inputs instead of targets) will give the same result (but inverted) except for the ones that use avg target (SMA, DGW, Digishield, & LWMA). The difficulty forms of these four give different results because 1/avg(targets) is not exactly equal to avg(1/targets). By 1/target I mean difficulty = 2^256/target. To keep them perfectly the same when working in terms of difficulty like CN coins you could use the relation 1/avg(target) = harmonic_mean(difficulty). If targets (or difficulties) are constant then harmonic_mean = mean and it's all the same. Harmonic mean gives a lower value than the mean so algorithms that use avg(D) overshoot D, causing a little more instability and slightly longer solvetime as N gets small, otherwise it's the same.
Simplest Algorithm
This is probably the simplest DA that works surprisingly not-too-bad. It simply adjusts up or down 0.5% if solvetime was below or above median expected solvetime. It's based on the exponential distribution having 50% of solvetimes below 0.693*T if difficulty is set correctly.
if (st < 0.693 * T) { next_difficulty = prior_difficulty * 1.005; }
else { next_difficulty = prior_difficulty / 1.005;
Problems in the uncorrected forms of the algos:
ETH originally had a DA that someone intuitively guessed at that did not give the correct solvetime and had another problem. The updated Homestead version mostly corrected the two problems by very reasonable changes. My equation includes a ln(2) that shows a correct solvetime is derivable, despite only changing if solvetime is a multiple of T. It's an approximation of the "perfectly correct" ASERT not ony via the EMA approximation AND decimal round-off, but it's also the inverted form of the EMA that makes use of the additional approximation 1+x =~ 1/(1-x) for small x. This enables the possibility of negative of negative difficulties which is protected in ETH with a 99 factor. But that correction opens up the possibility if a >50% attacker's selfish mine getting 75% more blocks than a selfish mine in an algo that does not have a problem. My equation above corrects these errors and is discussed here.
DGW (Dark Gravity Wave) uses a horrendous loop calculation that is just an SMA that gives double weight to most recent target value which has almost no effect. I have an article on it here.
KGW (Kimoto Gravity Well) changes the size of the averaging window if solvetimes are too fast or too slow. It's a potentially very good idea, but no justification is used for the curve that decides when to use the smaller averaging windows. It seems to work OK. It has an out-of-sequence timestamp block that allows a catastrophic exploit if timestamps are not required to be sequential in the protocol. I'm not sure anyone is aware of this which seems to be a separate issue from past complaints. The BRNDF version in Zcoin prevents it from changing more than once per 12 blocks which should cause oscillations if there is a lot of switchable hashrate that could attack it, but Zcoin is not experiencing any problem while ranking "only" 107 in market capitalization ($28 M today, with BTC emission rate).
KGW and BRNDF reduce the SMA window to "i" blocks if the avg T/solvetime ratio is > A or < 1/A where A = 1+0.7048*(i/144)^(-1.228), and "i" might need to be at least some min like 36.
Digishield as usually implemented includes a 6-block delay in the window of the solvetimes it uses. This causes tolerable oscillations. (Grin's N=2 in my equations should be N=3) The reason for the delay is to make sure solvetimes are in sequence (which prevents a catastrophic exploit on timespan limits that BTC/LTC/BCH/KGW/DGW have). There are two other methods that could and should have been used to prevent the delay and therefore oscillations. The equation I have above does not include the delay. The delay makes it worse than merely ranking as low as KGW but both work better than SMA and coins do not usually see any problem with them. It also has 16% and 32% useless timespan limits that force a 500 block delay in it reaching the correct solvetime if difficulty changes a lot such as in genesis. I have an article on it here. The equation shown is completely unrecognizable to those familiar with it. I did it like this to show how it is similar to EMA. A more recognizable form with the identical math that more closely resembles the SMA is
next_target = avg(target) * ( 0.75 * T + 0.25 * (tN-t0)/N ) / T
BTC/LTC have several problems. Biggest problem is that it's not even an SMA rolling average. This has kept BTC 6.6% ahead of coin emission schedule due to difficulty always rising and it not responding fast enough. Small coins attempting this algorithm quickly realize they will have to fork to replace it. BTC has the Zeitgeist hole in it and BTC/LTC both have an additional N/(N-1) over-estimate in the difficulty (underestimate in target) due to the exponential distribution having more fast solvetimes than slow ones in a finite N sample. See this. Also, if difficulty is changing, the perfectly correct estimate of hashrate from a few blocks is
HR = harmonic_mean(Difficulties/solvetimes) * (N-1)/N
and this could be used to set the difficulty: next_target = HR * T. It is more accurate than SMA as a rolling average, but in response to "reactive changes" from miners in response to difficulty, it is worse.
SMA (Simple Moving Average) is more likely to have bad oscillations. The formally correct SMA is the following. It seems to not be better than the simpler SMA (maybe not even as good with changing hashrate). But under constant hashrate conditions, it's the only SMA that gives the correct avg st all the way down to small N=3.

Monero / Cryptonote is an SMA but some awful modifications were made. All small and even most medium coins using it have to replace it. The problem is that it has a cut and lag that prevent it from considering recent solvetimes especially under on-off mining conditions. This results in oscillations that are not merely stable as in Digishield and an SMA. The oscillations can amplify, typically resulting in a small coin getting stuck. My LWMA became well-known as coins abandoning this algo became aware of similar cryptonote coins using LWMA.
EMA/ASERT are the preferred algorithm, but you have to be careful in using it. Cryptonote coins can't use it because they have a 1 block delay in the timestamps. I have an article here that in part discusses all the potential problems. "EMA" comes from Jacob Eliosoff's attempt to create an EMA for DAs. I noticed it closely resembles a section in Wikipedia. Tom Harding and Kyuupichan worked to improve it and ended up with the simpler form I show above that is nearly as accurate but does not need the e^x function. Jacob also thought of the ASERT but did not pursue it due to the similarity and e^x. Mark Lundeberg and Dragos Ilie et al (Imperial College) independently thought of ASERT. Amazingly, it needs only the current timestamp (t) and the genesis block's difficulty (Dg) and timestamp (tg), i.e. D = Dg * e^((N*T-(t-tg)/M) which we call "absolute ASERT" that Mark & Imperial College independently showed is mathematically equal to the relative ASERT. Absolute prevents round off error in the approximate e^x calculation and the error in nBits round off. The round-off error in e^x approximation or target (at times nBits's error can be 2^(-15) = 0.003% error) is multiplied by N*M. The e^x error can be greatly reduced by changing the target block time T by the same amount to cancel error*N*M. The error is 1.5% at times due to nBits if N*M = 500, but you can't simply correct for it without checking in the difficulty algorithm how much error nBits currently has. Mark and I prefer EMA (which is an approximation of relative ASERT) for it's simplicity as long as N is not too large to keep these errors low. BTW, there are several other names for M or 1/M (aka "alpha" in EMAs) in various fields of science like survival or extinction coefficient, time constant in an RC filter, turbidity coefficient for light passing through gases or liquids, and "half life" if 2^(-t/M) is used. In this case, M is a "turbidity" or "filter" to the difficulty adjusting to the correct value in response to a hashrate change. Mark shows in this tweet the best way to calculate e^x which Jonathan Toomin implemented in BCH's ASERT. Jacob Eliosoff was the first one to briefly consider ASERT as shown here.
See LWMA below for EMA/ASERT's only problem.
LWMA in terms of difficulty is this:
D[h+1] = avg_D[ h to h-N+1] * T * (N*(N+1)/2) / k[h] eq (1)
k[h] = linear weighting of solvetimes = 1*st[h-N+1] + 2*st[h-N+2] + ... N*st(h]
The (N*(N+1)/2) scales the above linear weightings back down to an "average".
An algebra trick to avoid a loop for D[h+2] appears to be to solve for k[h] in D[h+1] and do this:
k[h+1] = k[h] - sum_st[h-N+1 to h ] + N * st[h+1] eq (2)
A loop can be avoided because:
sum_st[h-N+1 to h ] = t[h] - t[h-N]
avg_D[ h to h-N+1] = ( CD[h] - CD[h-N] )/ N
where CD = cumulative difficulty.
Substituting and using eq 2 for the next block::
D[h+2] = (CD[h+1] - CD[h-N+1] )/ N * T * (N*(N+1)/2) / k[h+1]
An initial loop needs calculated very precisely to initialize this.
Using M = (N+1)/2 and rewriting can show why it's somewhat like EMA and therefore ASERT:
D[h+1] = avg_D[h] / (avg_D[h-1]/D[h] + st[h]/T/M - avg_st[h-1]/T/M )
* This is calculated by time-weighted attacker's average target divided by time-weighted avg of all targets. That is, % unfair gains = sum(target_when_attacker_was_active * time_at_attackers_target) / sum(each_target*time_at_each_target/total time) . The specific test for the rankings used a miner motivation equation to model the apparent motivation in BCH's 2019 on-off mining problem. Specifically, it says "Begin 6x avg hashrate mining if difficulty (1/target) is 130% of average difficulty that the 1x hashrate miners would have if there was no on-off mining, and stop when it is 135%. I also ran other tests such as start and stop on 95% and 105%.
Latex for the equations:
\text{t = timestamp, tar = target, T = desired blocktime , h=height}\\
\text{st = solvetime, i.e.} \ \ st_h =t_{h} - t_{h-1} \\
next\_tar = prior\_target\ *\ \frac{t_N-t_1}{NT} \text{ (BTC)} \\
next\_tar = prior\_target\ *\ \frac{t_N-t_0}{NT}*\frac{N}{N-1} \text{ (BTC with 2 corrections)} \\
tar_{h+1} = \frac{1}{NT}\sum_{i=1}^{N} \left[tar_i*(st_i) \right] * \frac{N}{N-1}
\text{ (Time-weighted SMA * Erlang correction)} \\
tar_{h+1} = avg\_N\_targets\ *\ \frac{t_N-t_0}{NT} \text{ (SMA, DGW's loop simplified) } \\
\text{If past i blocks were too fast or too slow, reduce N to i in above SMA. (KGW, BRNDF)} \\
tar_{h+1} = avg\_N\_targets\ *\ (1\ + \frac{t_{N}-t_{0}}{MTN} - \frac{1}{M}) \text{ (Digishield M=4, Grin M=3) } \\
tar_{h+1} = tar_h*(1+\frac{st_h}{MT} - \frac{1}{M})\text{ (EMA) } \\
tar_{h+1} = tar_h\ *\ (1\ +\ int(\frac{st_h}{T*ln(2)})*\frac{1}{M}\ -\ \frac{1}{M})\text{ (ETH with ln(2) for st accuracy) } \\
tar_{h+1} = avg\_N\_targets\ * \frac{2}{N(N+1)T}\sum_{i=1}^{N} i*st_i \text{ (LWMA) } \\
tar_{h+1} = tar_h*\left[e^{(t_h-t_{h-1})/T - 1} \right]^\frac{1}{M} \text{ (relative ASERT) } \\
tar_{h+1} = tar_H*\left[e^{(t_h-t_{H-1})/T - (h-H)} \right]^\frac{1}{M} \text{ (absolute ASERT, H=beginning block height) } \\
sub\_tar_{h+1} = \text{SlowASERT}*\left[e^{(t_{h+1}-t_h)/T - 1} \right]^\frac{1}{P} \\ \text{ (TSA RTT with SlowAsert * Fast RTT ASERT)}
Discussion of why and in what sense ASERT is the "perfectly correct" difficulty algorithm.
The other algorithms are just approximations to what ASERT does. EMA is very close to ASERT as can be seen by using the approximation e^x = 1+ x in ASERT to get EMA which is valid for small x (e.g. M>20). The corrected ETH algorithm is an integer truncation of the EMA that gives surprisingly acceptable results. ASERT was devised by Mark Lundeberg @markblundeberg (he'll publish a public PDF on it sometime). ASERT appears to be the ratio of the expected to the observed solvetime distributions. That is, in terms of targets, it's e^-1 divided by e^(-solvetime/T). There is also a "smoothing" power factor of 1/M to make it more stable (aka respond more slowly). Intuitively, the 1/M appears correct because adjusting the target every block uses multiplication that builds upon past multiplications of the roots of the ratios. ASERT's expected maximum rate of change is a factor of e in M blocks. LWMA rises about 50% faster and falls about 50% more slowly, which can be good and bad.
ASERT is the only algorithm that gives the perfectly correct solvetime no matter how slow or fast it is made to respond by adjusting the M factor, and no matter how much hashrate changes, except it gets behind M blocks for every 2.718x permanent increase in hashrate. All algorithms will have that type of except for a dangerous one that predicts increases in hashrate and thereby trying to adjust ahead of time. BTC/LTC can also get the correct long term average solvetime if a N/(N-1) correction factor in target is applied, but it is not as accurate on a per block basis because it is not changing every block, and there does not appear to be a valid adjustment for N=1 (a division by zero) that ASERT can do. The N/(N-1) is an explicit correction factor. All the algos can similarly get the correct long-term average solvetime if a correction factor based on N and/or solvetime is applied, but this appears to be approximating ASERT. Also, all the algos that use more than just the previous target like ASERT, EMA, and ETH will give a different result if there is an attempt to apply the inverse of the equation directly to difficulty. To get the same result they have to use the harmonic mean of difficulties which gives the mean target. These are my observational and pseudo-theoretical argument for why ASERT is the only mathematically correct difficulty algorithm, assuming we do not make assumptions or predictions about miner motivation.
UPDATE:
A new algo "CDF-EMA" is mathematically more pure than ASERT and it may be better in a strict sense. The image below shows an error signal that it uses which is mathematically better than ASERT's "1-t/T". It's better at preventing on-off mining from getting excess rewards over dedicated miners but at a cost of making the average solvetime a little longer during on-off mining. It's mathematically more pure because it takes probabilities into account. It works at a micro level where ASERT works on a macro level. ASERT targets an average solvetime, overshooting the individual estimate of hashrate (and thereby the adjustment) when a solvetime is fast, and undershooting when it's slow. At the micro level, we have 1 sample per block, so we "expect" the median solvetime which is when CDF=0.5 which is a solvetime of t = ln(2) * T (where t= solvetime and T=block time). The CDF (of the exponential function in our case) is a uniform distribution that we can use to measure how much the solvetime was unexpected. Since it's uniform, it's a linear adjustment in the "space" of P. It maps the nonlinear t's that we expect from our previous estimate of hashrate to a linear space, making it an excellent error signal for adjustment. I tested many different ways of using this error signal and the one below is simplest and most stable. The "3" in the exponent is an approximate value that makes its level of filtering about equal to ASERT's (it could be changed to "1"). The "3" shows it needs less filtering (a smaller effective N) to get the same level of precision in average solvetime without even targeting average solvetime over a longer time ("macro") like ASERT does. For small filter values (small N) CDF-EMA has a small error in the median and mean where ASERT has 50% error in the median while targeting the mean perfectly. Given the CDF of any distribution, this equation is a good method of prediction and control. A concerning drawback is that it assumes timestamps follow the exponential distribution. For example of how this is a problem, if every miner selects a timestamps such that t=T, the difficulty gets easier & easier. The consequences of this are complicated but not necessarily a problem.
Update 2
I discovered a surprisingly simple algo that works as good as the best.
next_target = prior_target * (0.56 * T/t)^(1/N)
N is on the order of LWMA's N (see section on how to make the algos have the same stability). Since prior solvetime t is in the denominator, monotonic timestamps have to be enforced to prevent divide by zero or an imaginary result.
A Time-Based Algorithm
This is an algorithm based on a time window instead of a block window. It adjusts once every N * blocktime. Ideally it would use RTT with tight timestamp rules.
D = prior_D * (C/(N-1))^(1/M)
where C = blocks observed in past N * blocktime seconds from a miner's local clock that he uses as the timestamp (in RTT he sets his own difficulty by his timestamp). For example, if N=6 for blocktime=10 minutes it means difficulty changes once every hour on the hour, enabling miners to affect their difficulty within the limits of the 1/M smoothing factor. The unusually wide range of timestamps BTC allows can't be used with this. Instead of 7200 s into the future and about 1 hour in the past (the MTP) like BTC, the allowable timestamps could be +/- 10 s from local time but few believe it (see my article on selfish mining)). An alternatively to the miner using local time (to avoid it being an RTT) is to use the prior timestamp. The prior block would not count as part of N, but its difficulty would be used as the prior_D. The results aren't as good. To partially alleviate this, the adjustment could be done only once per N blocks. The N-1 is because "the poisson is memoryless" both forward & backwards in time (credit Jacob Eliosoff). For example, if you pick any 2 * blocktime range at some random point in time, the average number of blocks you'll see in the window is surprisingly 1 (it's because long solve times have a large effect). For 3 * blocktime the average number will be 2 blocks. Similarly, pick any random point time and the expected time between the 2 blocks on either side of that time is 2 * blocktime.
end updates
The Dynamic LWMA is here:
https://github.com/zawy12/difficulty-algorithms/wiki/Dynamic-LWMA
Use this page to discuss the LWMA if you are not part of our Discord channel.
This is not completely without any drawback. It does the following on accident once every 720 blocks (once per day for T=120). This is a 2x jump in difficulty for 4 blocks.
Summary: This discusses how bad oscillations can develop in simple moving averages. There is a follow-up article. See also these tweets for how the oscillations can be stopped by changing target during the block instead of changing to LWMA.
Update: in this article I mention the SMA oscillations are primarily due to not taking a slope into account. In testing that does seem to make the oscillations more chaotic (less like simple oscillations) and it does end the attacks quicker, but if miners do not have a high cost of switching coins, it's a worse algo because it drops to an attractive difficulty a lot more often, decreasing the benefits.
BCH uses a simple moving average (SMA) difficulty algorithm (DA) with N=144, which is a 1-day averaging wnidow for its T=600 seconds. Monero/Cryptonote clones suffered greatly from a similar long average, but that DA also had a "cut" and "lag" that prevented it from considering approximately the most recent approx 1.5 hours of block timestamps. Other issues in this series show how bad they were.
Forced delays in response cause positive feedback => bad oscillations
Monero/Cryptonote clones were suffering because if a situation develops where there is a sudden increase in hashrate (such as a price increase & there is a large source of hashrate external to your coin), then a lot of miners jump on and it takes the DA a long time to respond. When they leave from the difficulty getting too high, the difficulty is supposed to start dropping right away from solvetimes getting longer. But if there is an additional delay in looking at most recent solvetimes like Monero/Cryptonote's DA, it will keep rising, possibly above its pre-attack starting point, causing even your "dedicated" miners to leave. Eventually hashrate will drop but due to not seeing the loss of miners right away, it will also overshoot the downside like it did on the upside. This will cause even more miners to come back to mine, and the oscillations can "blow up" due to the positive feedback loop.
Although this chart is hard to see, it is a typical Monero/Cryptonote clone "blow up". Every small clone had to abandon this 24 hr SMA that had the "cut" and "lag" delays. The black line is difficulty. Note that it is 1 cycle per 24 hours. Blue are delays, magenta is hashrate increase.
Asymmetrical adjustments to difficulty can be harmful (remember EDA?)
This is kind of off-topic since the new DAA does not have asymmetrical adjustments like the previous EDA. Delays from being slow (not just from the CN-type forced delays above) can make oscillations from asymmetry in difficulty adjustment much worse. But even if there is no delay, asymmetrical adjustments will result in too fast or too slow coin emission, depending on "which side" of the adjustment has the asymmetry. Asymmetry can be defined as taking the "expected value" of the PDF of the algorithm and not getting the target solvetime (credit to Tom Harding @dgenr8 for showing me this) but this may not give reliable results if the algorithm changes itself (the PDF changes) based on an unpredictable hashrate, as did the EDA. Even BTC is "asymmetrical' in this sense because calculating the expected value to get T=600 assumes the hashrate is approximately constant, or moving up and down around an average, not always increasing like it has been. This has resulted in 6.5% faster blocks on average ( there are 2 other very minor errors in it ). As many recall, BCH's previous DA before late 2017 was the "EDA" that tried to drop a lot if the chain appeared to be getting stuck with long solvetimes. It did this because it was forking from BTC, expecting large decrease in hashrate. The big drops caused a sizeable influx of hashrate, and because it kept BTC's N=2016 adjustment (not a rolling avg) it was a long time before the DA knew it needed to increase hashrate. BTC's DA does not have the same kind of delay described above for default CN coins. It does not simply ignore the most recent timestamps. When it changes, it uses the most recent timestamp, but it has a different type of very long delay in responding. The avg solvetime is what it was 2016/2 blocks in the past because it makes not adjustment for slope, causing it to be 6.5% too fast in coin emission due to hashrate generally increasing every 2 weeks. This made the asymmetry problem in BCH's previous EDA much worse than it needed to be.
BCH's new DA is not asymmetrical but has a mild forced delay
BCH does not have a "forced" delay like the default CN coin, but it seems to have a 3-block delay. If there is a long solvetime, it seems to take 3 blocks to start dropping. It explicitly has only the 1-block delay from using the median of past 3 block timestamps. This was a neat but sort of a good and sort of a bad decision trying to prevent most out-of-sequence timestamps from indicating a negative solvetime that could be up to 6 timestamps in the past, via the MTP(11) setting. The 2nd delay is what almost all coins have: the DA does not use the current solvetime in its calculation, but the previous block's solvetime. My TSA article) discusses changing it during the block. KMD (next fork), Mochimo, Coin2 (research only), and Xchange (defunct) are doing it, about to, or previously did. I seem to see a 3rd delay that may be the way block explorers are reporting data, so it's possibly not a delay, or the pool and/or miner code is using the start time of mining as the timestamp on a block instead of when the block was solved. CN coins do this, and it may be occurring in Zcash coins.
Taking the Slope of Hashrate into Account
In various places in this article I mention the importance of SMAs not taking the slope of the solvetimes into account. This helps get the current hashrate estimate Without it, an SMA is estimating what the hashrate was at 1/2 it's window in the past. This is 1/2 a day for BCH. All good algorithms in one way or another are trying to estimate current hashrate without over-shooting the estimate (which would cause oscillations). I call this "taking the slope into account". "Not overshooting" can be seen as a passive as opposed to active controller. An active controller should not be used because miners can actively look at difficulty and change hashrate in a non-linear fashion while a "non-A.I." active controller (one that does not actively learn miner motivation over time and change itself accordingly) has to make non-changing assumptions about miner (hashrate) motivation which miners will promptly deviate from to profit, at least at the expense of other miners if the DA is good at keeping coin emission rate correct. In summary, a non-smart active controller on a re-active system can blow up, but an estimate of current hashrate without making assumptions about miner motivation is safe, needed, and in all good DAs (not in SMAs like DGW). Due to the 6-block MTP delay in the default Digishield in estimating hashrate and it's N=17 part being an SMA average, it's about 6+17/2 = 15 blocks behind, and constantly suffers 15-block attacks with resulting mild oscillations.
Why does BCH have bad oscillations?
Despite no asymmetry, no sizable forced delay like CN, and being a rolling average, BCH is having bad oscillations. This is because miners have (probably unconsciously, see below) found a beneficial oscillating pattern based on the SMA window width. As the fast solvetimes of the previous hash-attack roll out the back of the averaging window, the difficulty will not change if there is currently another attack that has fast solvetimes. The solvetimes rolling out the back cancel the ones coming in the front. If there were not an attack, then difficulty would start dropping even if current solvetimes are correct, due to the fast solvetimes going out the back. In short, a 24 hour SMA difficulty is basically looking at difficulty how it was 12 hours in the past. so it has a delay that can cause oscillations. In BCH's case, bad oscillations are about 1/2 a day, 72 blocks, lasting 20 to 30 blocks, then stopping for a few blocks with long delays, difficulty dropping some, then a short attack, then a few slow blocks, then another big attack about 72 blocks after the previous attack. That is the pattern seen now in September 2019. Back in July 2019, there were some oscillations about half as bad, and it was a 144-block cycle.
Modelling the Above Attack Oscillation
The following is modelling that simply says "if difficulty is 1% below avg, then begin mining with 6x avg hashrate and stop when it reaches the average." Notice this simple logic discovers the oscillations and the attacker has about 5% lower-than-average difficulty ("sudden" ~10% drops appear when the previous fast attack solvetimes roll out the back of the window) while the miners staying after the attack have about 5% higher-than-avg difficulty (for that attack=off time period).
Below is the same miner motivation scenario with LWMA DA instead of the SMA N=144, which takes the slope into account, so solvetimes rolling out the back of the window do not cancel the ones entering the front, preventing the oscillations. It's 3x faster in rising, but this is not necessarily a benefit because it drops fast too, so the attacks are coming much more frequently in LWMA than above. The attackers may be able to get the same profit as before (since they should be able to change what coin they are mining very quickly), and the dedicated miners lose the same. But they are stopped so quickly, there are no long delay problems (BCH is only getting 3 blocks per hour or worse when the attacks stop).
In the previous issue BCH needs a new DA I discuss the source of oscillations in DAs. This details the source of those observations.
Summary: Simple Moving Average (SMA) difficulty algorithms cause dying oscillations in difficulty in response to sudden hashrate changes due to not taking the slope of solvetimes into account. Miner "momentum" or "friction" to joining and/or leaving (hysteresis) due to reward/difficulty ratio changes can sustain an oscillation who's size is related to the amount of momentum. The "momentum" in this context partly refers to the number of blocks delayed until a hashrate change, but is related more to the size of the hashrate change. A one-block delay with 5x hashrate change can sustain a sizable oscillation indefinitely, allowing the attacker to get lower-than-average difficulty. Profit margins due to better or worse reward/difficulty ratios can attract or dissuade an "exponential" (i.e. some non-linear function) amount of hashrate, so a 5x hashrate change is not unusual in small coins. The non-linearity in the relationship between hashrate and reward/difficulty is a major contributing cause of oscillations. Bad oscillations are caused in all algos if large miners stay on beyond the point that makes sense in terms of profit, and come back before it has dropped low enough for other miners to be interested. Bad oscillations are also caused by algorithms that do not use the most recent solvetimes in the averaging window, especially in SMAs. This causes positive feedback which can get the chain stuck as has happened in basically all Cryptonote/Monero clones that have a ~5% delay from "cut" and "lag". Forced delays can also cause mild oscillations in fast algorithms that are only partially a SMA (Digishield with a 6-block MTP delay, 10% of its 17x4 effective window). The oscillations in SMA's are a harmonic of the difficulty window averaging, cycling at 1x, 2x, or 3x the number of blocks in the window due to fast solvetimes rolling out the back of the window, canceling the effect of new fast solvetimes, keeping difficulty stable during a subsequent attack.
SMAs perpetuate oscillations in hashrate (aka on-off mining, aka hash-attacks) when there is non-dedicated hashrate available. If price suddenly rises there can be a large influx of hashrate. Hashrate is a nonlinear function of reward per difficulty due to a small increase in the ratio being a substantially larger profit margin. The converse applies if price falls. By not taking the slope of hashrate (usually by just looking at solvetimes instead of the more precise hashrate =1/avgTarget/avgSolvetime*(N-1)/N ) BTC & SMAs are estimating the hashrate as it was at the midpoint of their averaging window in the past. There's an inherent delay. If there is a substantial hashrate change the difficulty will reach the correct value faster than the difficulty window because the hashrate increase is more than linear. If hashrate increases were linear with the reward (in exchange dollars) per difficulty ratio, then it would take longer than the difficulty window and an oscillation would not occur. But since a large hashrate increase occurs, it reaches the "break even with other coins" ratio sooner. Digishield benefits from this effect by from being 4x slower than its averaging window of N=17. SMA & BTC reach break-even slowly, but not as slow as their full window from not taking slope into account, so miners have time to leaving without sending difficulty too high. By not taking slope into account, it almost can't overshoot unless a big miner has momentum for some reason and makes it overshoot, suffering a difficulty higher than is logically profitable, assuming he can switch coins easily & quickly. Algos with a slope adjustment must not overshoot on their own (EMA & LWMA do not), trying to predict miner behavior ahead of time.
Side Note: Momentum, Friction, and PID controllers in Difficulty
It should be assumed there is no momentum or friction in miner motivation (logical profit says there shouldn't be if he can change coins quickly... but often they do display momentum or friction i.e. they are slow to join or leave), so a PID or PD controller should not help because they are needed in cases of momentum and/or friction, and will cause oscillations if they assume there is momentum and/or friction when there is not (the D in PID is derivative aka slope and can have a constant that overshoots). Looking at recent past cycles to measure and remember momentum and friction and adjust accordingly seems like more complexity for DAs than should be used.....and opens a vulnerability: if it assumes or calculates miner behavior for the next few blocks and therefore responds ahead of time, miners will do the opposite to exploit it. But the fact that there is a kind miner momentum or friction or hysteresis in starting and stopping is the primary factor that causes oscillations in simple moving averages.
[newer comments on this:
SMA is like an electronic circuit or rod being struck that has a natural frequency of oscillation. N=144 SMA has harmonics at 144, 72, 36 and even 18-block cycles at times. It does not "cause" oscillations any more than a rod causes oscillations in itself. The problem is that it does not stop ringing if "struck" with a price change or a big miner making a somewhat random decision to start or stop mining. It does not inject an assumption like feed-forward controller, try to predict the future ("D" in PID), or add "energy" like the "i" and "D" gain constants in a PID controller. It's passive. Price changes or miners inject the "energy" that causes it to ring.
RC filters seem like a good parallel to ASERT's "low-pass filter" parameter, but the math does not indicate a good parallel. Vout = Vin * (1-e^(-t/RC)) instead of next_D = previous_D * [e^(-t) / e^(-1) ]^(1/N) where N = mean lifetime = "RC". ( I've scaled t/T in ASERT to just a "t" in blocks unit and N is in blocks because R and C units are already scaled to its "t" seconds. )
end update ]
Getting back on track...
Continuing where I left off, let's assume we have the common situation where a fairly sudden and large hashrate increase (> 2x hashrate baseline) has increased difficulty to match an exchange price increase. Many of the original opportunists will leave as it rises because they typically have a default or preferred coin, so it can even out smoothly. But sometimes miners can have momentum to staying aka friction to leaving aka 1/2 of a hysteresis in reverting to their previous coin, causing it to overshoot which can begin an oscillation. But I'll assume that does not occur. Everything is fine until those fast solvetimes that mark the beginning of the hashrate increase start to roll out the back of the averaging window. Difficulty will start to drop despite it currently being at the correct level. To keep difficulty stable, miners would have to solve blocks just as fast as the original hash-attack, but they can't because difficulty is near the correct level instead of being way low, so it must continue drop,at the same rate it rose, if miners rejoin at the same rate they left. a symmetrical rise and fall like this without miner momentum will oscillate maybe only a little for one cycle and not be noticeable in the 2nd cycle (2x to 3x the window length). Miner momentum that lets difficulty rise or drop "too far" will sustained an oscillation that will be limited to the amount of the momentum. The momentum is a function of both the number of blocks delayed to a response, and the size of the response.
Sustained oscillations caused by momentum are exacerbated by the non-linearity of hashrate changes caused by slightly more (or less) profit being attractive to a LOT more (or less) hashrate). It is common in alts to see 3x more hashrate join when there is a 30% drop in difficulty, and it can go to 1/3 when difficulty is 30% higher.
The summary above mentions an algorithm may not look at the most recent solvetimes and this has the same effect of miner momentum, but unlike miner momentum instead of just sustaining an oscillation that is "proportional" to the momentum, it can draw in more hashrate with each cycle (positive feedback) by overshooting to the upside and downside until the chain is stuck. An algorithm that uses the slope can prevent that error from getting out of control. To explain this effect further: miner motivation that is delayed (the"delay to respond" part of their "momentum") is self-correcting: it will cause the difficulty to drop further in a cycle, but as it drops further, that delay is reduced due to desire for the higher profit. A fixed 10-block delay in what solvetimes are included will still be there no matter how low the difficulty drops, or rises.
BTC adjusting only once per 2016 blocks is a 1-week delay in measuring current hashrate, but it's not a delay that ignores the most recent solvetimes when it changes, so it does not amplify oscillations. It certainly is not as good as a simple moving average, but it also does not have the SMA effect of the previous attack's solvetimes rolling out the back of the window preventing difficulty from rising during a current attack. But it can definitely have an oscillation from the non-linear amount of hashrate that comes and goes in response to difficulty. It could perpetually overshoot and undershoot alternatively every 2016 blocks.
All these oscillations are only present when there is "non-dedicated" hashrate that can come and go, and usually requires > 2x the baseline hashrate for it to be noticeable.
This article was motivated by my recent observations of BCH. It is a good case study. The difficulty was not changing much (+/- 5%). The miners were not waiting for difficulty to drop much at all (small momentum). The hashrate changes were not super large (compared to small coins I deal with). They were "only" about 6x the average (about 12x the "dedicated" miners). So the delay*hashrate change factor for momentum was not really big. There is a forced delay in the algorithm that adds some positive feedback, but it's only 2 blocks on a window of 144 (1.5%), not like Cryptonote's 6% (~45 blocks on N=720). But BCH and Cryptonote are 24 hour windows. Really time has no effect in the math, but the number of blocks. But time has a big effect on the reward/difficulty ratio, so we can expect bigger prices changes per difficulty window size which kicks off the oscillations.
Update: When I wrote the above 3 days ago I could see the harmonics of BCH oscillations had an element of 3 cycles per 144 blocks, but the major swings were 2x per days. It looked like BCH was in serious danger. But then the 3rd harmonic got a lot bigger and seems to have helped reduce the other swings by "taking energy away from them". The following chart shows the 3rd harmonic clearly picking up and seeming to take some steam out of the others. Notice it is a log scale, so these are not minor swings.
The following chart with a linear scale and a longer averaging period to smooth things out shows how the severity of the situation was reduced.
This chart is from the summer shows only 1 cycle per 144.
I was able to partially model the 2nd harmonic BCH oscillations by specifying a miner motivation rule that said "if difficulty is <130% of what the baseline (dedicated) hashrate alone would have, then begin 8x hashrate, and stop when it is 132%. " Miners are probably joining and slowly than this simple on-off, which could be a way to model the 2nd harmonic better. The on-off miners get an avg difficulty 5% below avg while the other miners have to pay 5% above avg.
Using LWMA with the same miner motivation profile did not have any oscillations. This is not proof that 8x hashrate can't find a way to get unfair profit (compared to dedicated miners) out of LWMA, but the difficulty in doing so by modelling, and knowing Cryptonote's 24 hr avg was terrible, is why I've recommended it.
CN coins: The last test of your fork is to make sure your new difficulties when you sync from 0 are matching the old difficulties when running the pre-fork code. See this note.
FWIW, it's possible to do the LWMA without looping over N blocks, using only the first and last difficulties (or targets) and their timestamps. In terms of difficulty, I believe it's:
ts = timestamp D_N is difficulty of most recently solved block.
D_{N+1} = next_D
S is the previous denominator:
S = D_N / [ D_{N-2} + D_{N-1}/N - D_{-1}/N ] * k * T
k = N/2*(N+1)
D_{N+1} = [ D_{N-1} + D_N/N - D_0/N ] * T * k /
[ S - (ts_{N-1}-ts_0) + (ts_N-ts_{N-1})*N ]
I discovered a security weakness on 5/16/2019 due to my past FTL recommendations (which prevent bad timestamps from lowering difficulty). This weakness aka exploit does not seem to apply to Monero and Cryptonote coins that use node time instead of network time. If your coin uses network time instead of node local time, lowering FTL < about 125% of the "revert to node time" rule (70 minutes in BCH, ZEC, & BTC) will allow a 33% Sybil attack on your nodes, so the revert rule must be ~ FTL/2 instead of 70 minutes. If your coin uses network time without a revert rule (a bad design), it is subject to this attack under all conditions See: zcash/zcash#4021
People like reading the history of this algorithm.
Comparing algorithms on live coins: Difficulty Watch
Send me a link to open daemon or full API to be included.
See LWMA code for BTC/Zcash clones in the comments below. Known BTC Clones using LWMA: are BTC Gold, BTC Candy, Ignition, Pigeon, Zelcash, Zencash, BitcoinZ, Xchange, Microbitcoin.
Testnet Checking
Emai me a link to your code and then send me 200 testnet timestamps and difficulties (CSV height, timestamp, difficulty). To fully test it, you can send out-of-sequence timestamps to testnet by changing the clock on your node that sends your miner the block templates. There's a Perl script in my github code that you can use to simulate hash attacks on a single-computer testnet. Here's example code for getting the CSV timestamps/difficulty data to send me:
curl -X POST http://127.0.0.1:38782/json_rpc -d '{"jsonrpc":"2.0","id":"0","method":"getblockheadersrange","params":{"start_height":300,"end_height":412}}' -H 'Content-Type: application/json' | jq -r '.result.headers[] | [.height, .timestamp, .difficulty] | @csv'
Discord
There is a discord channel for devs using this algorithm. You must have a coin and history as a dev on that coin to join. Please email me at [email protected] to get an invite.
Donations
Thanks to Sumo, Masari, Karbo, Electroneum, Lethean, and XChange.
38skLKHjPrPQWF9Vu7F8vdcBMYrpTg5vfM or your coin if it's on TO or cryptopia.
LWMA Description
This sets difficulty by estimating current hashrate by the most recent difficulties and solvetimes. It divides the average difficulty by the Linearly Weighted Moving Average (LWMA) of the solvetimes. This gives it more weight to the more recent solvetimes. It is designed for small coin protection against timestamp manipulation and hash attacks. The basic equation is:
next_difficulty = average(Difficulties) * target_solvetime / LWMA(solvetimes)
LWMA-2/3/4 are now not recommended because I could not show they were better than LWMA-1.
Use this if you do not have NiceHash etc problems.
See LWMA-4 below for more aggressive rules to help prevent NiceHash delays,
// LWMA-1 difficulty algorithm
// Copyright (c) 2017-2018 Zawy, MIT License
// See commented link below for required config file changes. Fix FTL and MTP.
// https://github.com/zawy12/difficulty-algorithms/issues/3
// The following comments can be deleted.
// Bitcoin clones must lower their FTL. See Bitcoin/Zcash code on the page above.
// Cryptonote et al coins must make the following changes:
// BLOCKCHAIN_TIMESTAMP_CHECK_WINDOW = 11; // aka "MTP"
// DIFFICULTY_WINDOW = 60; // N=60, 90, and 150 for T=600, 120, 60.
// BLOCK_FUTURE_TIME_LIMIT = DIFFICULTY_WINDOW * DIFFICULTY_TARGET / 20;
// Warning Bytecoin/Karbo clones may not have the following, so check TS & CD vectors size=N+1
// DIFFICULTY_BLOCKS_COUNT = DIFFICULTY_WINDOW+1;
// The BLOCKS_COUNT is to make timestamps & cumulative_difficulty vectors size N+1
// If your coin uses network time instead of node local time, lowering FTL < about 125% of
// the "revert to node time" rule (70 minutes in BCH, ZEC, & BTC) will allow a 33% Sybil attack
// on your nodes. So revert rule must be ~ FTL/2 instead of 70 minutes. See:
// https://github.com/zcash/zcash/issues/4021
difficulty_type LWMA1_(std::vector<uint64_t> timestamps,
std::vector<uint64_t> cumulative_difficulties, uint64_t T, uint64_t N, uint64_t height,
uint64_t FORK_HEIGHT, uint64_t difficulty_guess) {
// This old way was not very proper
// uint64_t T = DIFFICULTY_TARGET;
// uint64_t N = DIFFICULTY_WINDOW; // N=60, 90, and 150 for T=600, 120, 60.
// Genesis should be the only time sizes are < N+1.
assert(timestamps.size() == cumulative_difficulties.size() && timestamps.size() <= N+1 );
// Hard code D if there are not at least N+1 BLOCKS after fork (or genesis)
// This helps a lot in preventing a very common problem in CN forks from conflicting difficulties.
if (height >= FORK_HEIGHT && height < FORK_HEIGHT + N) { return difficulty_guess; }
assert(timestamps.size() == N+1);
uint64_t L(0), next_D, i, this_timestamp(0), previous_timestamp(0), avg_D;
previous_timestamp = timestamps[0]-T;
for ( i = 1; i <= N; i++) {
// Safely prevent out-of-sequence timestamps
if ( timestamps[i] > previous_timestamp ) { this_timestamp = timestamps[i]; }
else { this_timestamp = previous_timestamp+1; }
L += i*std::min(6*T ,this_timestamp - previous_timestamp);
previous_timestamp = this_timestamp;
}
if (L < N*N*T/20 ) { L = N*N*T/20; }
avg_D = ( cumulative_difficulties[N] - cumulative_difficulties[0] )/ N;
// Prevent round off error for small D and overflow for large D.
if (avg_D > 2000000*N*N*T) {
next_D = (avg_D/(200*L))*(N*(N+1)*T*99);
}
else { next_D = (avg_D*N*(N+1)*T*99)/(200*L); }
// Optional. Make all insignificant digits zero for easy reading.
i = 1000000000;
while (i > 1) {
if ( next_D > i*100 ) { next_D = ((next_D+i/2)/i)*i; break; }
else { i /= 10; }
}
return next_D;
}
The following is an idea that could be inserted right before "return next_D;
// Optional.
// Make least 2 digits = size of hash rate change last 11 BLOCKS if it's statistically significant.
// D=2540035 => hash rate 3.5x higher than D expected. Blocks coming 3.5x too fast.
if ( next_D > 10000 ) {
uint64_t est_HR = (10*(11*T+(timestamps[N]-timestamps[N-11])/2)) /
(timestamps[N]-timestamps[N-11]+1);
if ( est_HR > 5 && est_HR < 25 ) { est_HR=0; }
est_HR = std::min(static_cast<uint64_t>(99), est_HR);
next_D = ((next_D+50)/100)*100 + est_HR;
}
This is LWMA-2 verses LWMA if there is a 10x attack. There's not any difference for smaller attacks. See further below for LWMA compared to other algos.
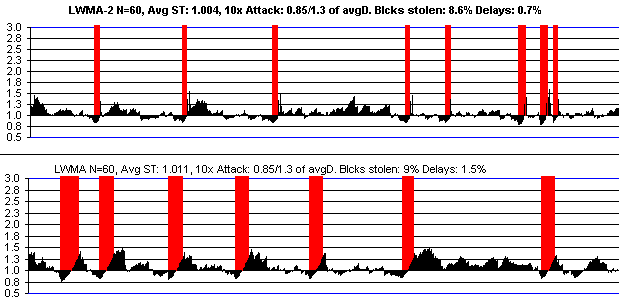
Credits:
Known coins using it
The names here do not imply endorsement or success or even that they've forked to implement it yet. This is mainly for my reference to check on them later.
Alloy, Balkan, Wownero, Bitcoin Candy, Bitcoin Gold, BitcoiNote, BiteCode, BitCedi, BBScoin, Bitsum, BitcoinZ(?) Brazuk, DigitalNote, Dosh, Dynasty(?), Electronero, Elya, Graft, Haven, IPBC, Ignition, Incognito, Iridium, Intense, Italo, Loki, Karbo, MktCoin, MoneroV, Myztic, MarketCash, Masari, Niobio, NYcoin, Ombre, Parsi, Plura, Qwerty, Redwind?, Saronite, Solace, Stellite, Turtle, UltraNote, Vertical, Zelcash, Zencash. Recent inquiries: Tyche, Dragonglass, TestCoin, Shield 3.0. [update: and many more]
Importance of the averaging window size, N
The size of of an algorithm's "averaging" window of N blocks is more important than the particular algorithm. Stability comes at a loss in speed of response by making N larger, and vice versa. Being biased towards low N is good because speed is proportional to 1/N while stability is proportional to SQRT(N). In other words, it's easier to get speed from low N than it is to get stability from high N. It appears as if the the top 20 large coins can use an N up to 10x higher (a full day's averaging window) to get a smooth difficulty with no obvious ill-effects. But it's very risky if a coin does not have at least 20% of the dollar reward per hour as the biggest coin for a given POW. Small coins using a large N can look nice and smooth for a month and then go into oscillations from a big miner and end up with 3-day delays between blocks, having to rent hash power to get unstuck. By tracking hashrate more closely, smaller N is more fair to your dedicated miners who are important to marketing. Correctly estimating current hashrate to get the correct block solvetime is the only goal of a difficulty algorithm. This includes the challenge of dealing with bad timestamps. An N too small disastrously attracts on-off mining by varying too much and doesn't track hashrate very well. Large N attracts "transient" miners by not tracking price fast enough and by not penalizing big miners who jump on and off, leaving your dedicated miners with a higher difficulty. This discourages dedicated miners, which causes the difficulty to drop in the next cycle when the big miner jumps on again, leading to worsening oscillations.
Masari forked to implement this on December 3, 2017 and has been performing outstandingly.
Iridium forked to implement this on January 26, 2018 and reports success. They forked again on March 19, 2018 for other reasons and tweaked it.
IPBC forked to implement it March 2, 2018.
Stellite implemented it March 9, 2018 to stop bad oscillations.
Karbowanec and QwertyCoin appear to be about to use it.
The competing algorithms are LWMA, EMA (exponential moving average), and Digishield. I'll also include SMA (simple moving average) for comparison. This is is the process go through to determine which is best.
First, I set the algorithms' "N" parameter so that they all give the same speed of response to an increase in hash rate (red bars). To give Digishield a fair chance, I removed the 6-block MTP delay. I had to lower its N value from 17 to 13 blocks to make it as fast as the others. I could have raised the other algo's N value instead, but I wanted a faster response than Digishield normally gives (based on watching hash attacks on Zcash and Hush). Also based on those attacks and attacks on other coins, I make my "test attack" below 3x the basline hashrate (red bars) and last for 30 blocks.
Then I simulate real hash attacks starting when difficulty accidentally drops 15% below baseline and end when difficulty is 30% above baseline. I used 3x attacks, but I get the same results for a wide range of attacks. The only clear advantage LWMA and EMA have over Digishield is fewer delays after attacks. The combination of the delay and "blocks stolen" metrics closely follows the result given by a root-mean-square of the error between where difficulty is and where it should be (based on the hash rate). LWMA wins on that metric also for a wide range of hash attack profiles.
I also consider their stability during constant hash rate.
Here is my spreadsheet for testing algorithms I've spent 9 months devising algorithms, learning from others, and running simulations in it.
Here's Hush with Zcash's Digishield compared to Masari with LWMA. Hush was 10x the market capitalization of Masari when these were done (so it should have been more stable). The beginning of Masari was after it forked to LWMA and attackers were still trying to see if they could profit.
Mark Freidenbach presented a low-pass filter idea for difficulty adjustment back in 2016 in this video and implemented it on Freicoin (which is now kind of dead). I immediately thought this was a bad idea (when I saw it in 2017) because there is no "noise" to be filtered. All the data points (solvetimes) are (exponentially) random, but relevant, not the result of noise from a an external forcing function that needs to be filtered. The EMA algorithm correctly converts the non-noise randomness back to linear data points. In the video, Mark and a questioner seem to think a higher-order filter would be better, but they would have the same problem. In a grander sense 2nd order calculations do not apply to difficulty because there is no mass-like variable with an inertia-like quality in difficulty as it is in physical systems (which I discuss in the PID controller for difficulty issue). Low pass filtering can apply to difficulty because on-off mining is a persistent problem in small coins, and that's akin to a radio picking up a click of static if a nearby large surge of current occurs. But that's not what the Freicoin algorithm is trying to address. Several of my algorithms do just the opposite of a low pass-filter: they increase difficulty as quickly as possible if an increase in hashrate occurs.
Lengthy Side Note: Electrical Signal Analogy to Hashrate
Simply taking a longer average is a low-pass filter, same as putting a coke inductor in series on a laptop's power cord (or a capacitor in parallel for the DC output of a power supply). Inductors and capacitors in these cases are storing energy, and difficulty is doing something very similar: measuring a true energy that is proportional to a number of hashes that occurred over it's averaging period. So the difficulty coming out is smoother. My fast-response add-ons to difficulty such as LWMA-3 or 4, fuzzy LWMA, and dynamic LWMA are even more like the inductor and capacitor but in a very different way: rather than trying to get difficulty to be smooth, they try to get solvetimes smooth. The sudden increase in difficulty is like the "ohmic reactance" of inductors and capacitors ("reactance" is the more general form of ohms of resistance, resistance to voltage change in capacitors and resistance to current change in inductance). The best analogy is somethinhashes are electrons and therefore hashrate is current and therefore responding with a higher difficulty to higher hashrate more quickly is like a larger inductor in series with the wire (network). Inductors are 1st order filters and 2nd order is warranted. In algorithms I used non-linear functions to detect and respond to the non-linear sudden hashrate changes which is high order.
The Algorithm
It looks at the past 144 blocks (1 day at T=600 seconds) and attempts to adjust once every 9 blocks. Not adjusting every block makes no sense. It seems to make it revert to its +/- 5% adjustment limits half the time, causing a bad sawtooth pattern, always above it's target solvetime.
The filter was supposed to assign weights to different solvetimes:

Y-axis is the weight and the x-axis are solvetimes. It gives more weight to near-average solvetimes (or maybe solvetimes closer to target) and less weight to high and low solvetimes. Below this plot was a plot of the frequency response where the low "frequencies" were allowed to pass through while the high frequencies were blocked. He said "low frequencies which represent the long term averages are passed through unchanged." I can't make sense of this or how the weighting factors of the first plot could lead to the "frequency" response of the second.
The weights are used to affect difficulty like this"
next_D = previous_D + previous_D*0.1025*(1-avgWeightSolvetime/TargetSolvetime)
For example, if solvetimes are faster, next_D will be increased more, so the direction of correction is correct.
[
2022 Update: The error factor (and all the equations that follow) needed to be
error = target/N * (0.5-e^(-t/T))
This tweet thread supersedes this article.
https://twitter.com/zawy3/status/1491958678852886554
And updated image here:
https://twitter.com/zawy3/status/1492150874348691459
The "I" controller is redundant to the filter on P=1/N & works for any process without needing to tune (you simply calculate CDF of your sensor variable from old data). All CDF's are uniform (linear) distributions. I found the best D controller to use is the gamma CDF for the prior 2 solvetimes minus the 2 solvetimes before that (and negated). Also, it turned out best in that case to use P=D=2.6/N where N is the filter that ASERT uses (the 2.6 gives it the same stability (Std Dev) as ASERT under constant hashrate. This image below specifies the best difficulty algorithm (a PD controller) that I've found, which is a specific implementation of the diagram above, keeping in mind the D part of the PD is using 2 pairs of solvetimes and putting them into the gamma CDF instead of the exponential CDF as indicated in the diagram. Using only the 2 previous solvetimes and exp CDF to get the slope seemed like it would be too unstable and experimentally this is what I saw. The gamma CDF is a better metric for more than 1 solvetime than trying to averaging two exponential CDF results, and experiment confirmed this statistical fact.
]
This derives a PID controller for difficulty and shows it is as good as the best (simpler) algorithms LWMAalgorithm and EMA algorithm.
Comparing PID to existing Algorithms
A simple moving averages seems like a PI controller in the sense there is a sum of past terms (the "I" part). LWMA, EMA, and Digishield give more weight to the more recent blocks which is like taking a slope into account which is the D part in a PID controller.
Derivation of PID Controller
Working directly in terms of difficulty gives bad results compared to working in terms of target. Target is the inverse of difficulty, i.e.
target = MaxTarget / difficulty (which I sometimes call 1/D).
A PID controller adds (or subtracts) to the previous setting a weighted sum of
Each is weighted by a multiplier constant (I'll call them p, i, d) that is determined by theory and/or experiment. A PID controller is therefore:
PID next_Target = prev_T + p*prev_Error + i*avg(prev_Errors) + d*slope(prev_Errors)
Notice the sum and slope are over some range(s). A wider window (larger N) will be more stable. To make p, i, and d consistent for changing window sizes, I found p & i need to be scaled by 1/N. This seems to keep p, i, & d in a -1 to 1 range. Notice the slope is already in "per block" terms, so maybe that is not scaling it by 1/N .
I will make a guess at a definition of the "error". The simplest I can think of is:
error = target*(ST/T - 1)
where ST=solvetime and T=target solvetime. So if ST is < T, this error is negative which will lower next_Target, making it harder solve like we want. And vice versa. Putting the above together:
PID Controller
next_T, prev_T, T[i] = target values
T = target solvetime
ST = solvetime.
p, i, and d are constants that give different weightings to each of the P-I-D terms.
PID next_T = prev_T + p/N*prev_Error + i/N*avg(Errors) + d*slope(Errors)
where p, i, and d are the weighting factors for the adjustments.
Error[i] = target[i]*(ST[i]/T-1) for i=1 to N blocks in past.
The above reasoning is not how I came across this. My route began with Jacob Eliosoff's suggestion of a certain type of EMA for difficulty. My testing of it showed it was perfectly correct for difficulty in some deep way. It works great and keeps perfect solvetime better than any other algorithm. Then Tom Harding (and Neil Booth) came up with a different type of EMA. I showed it was actually an approximation of Jacob's and was almost exactly the same. That made me think back to a book I had come across (image below) that said an EMA (not necessarily Jacob's or Tom's) could be used as a PID controller. So I started with Jacob's to get the PID like the book said, and used the simplification (see below). I forgot an old lesson and first worked it in difficulty instead of target. I got it to work in a tortuous way, then later corrected that mistake. Months later when trying to simplify this article I realized the end result could have been discovered by the above reasoning. The above PID does not need the exact EMA, as long as it's not trying to be a super fast algorithm. The simplification uses e^x = 1+x for small x where x=ST/T/N. As long as N >10 ish, x is small.
I now see EMA turns out to be close to a P-controller:
EMA next_target = N/(N-1)*prev_target + 1/N*prev_target *(ST/T-1)
except for the N/(N-1) factor, which makes a big (catastrophic) difference if it is removed in the EMA. Conversely, briefly trying to use the N/(N-1) in the PID controller seemed to make things worse, and that would be going against the precise derivation below.
The rest of this article was written months ago and it shows my tortuous process.
Summary:
# This is targeted to replace Zcash's Digishield with equal stability and 5x fewer delays
# See bottom for complete algorithm.
p=1, i=-0.15, d=0.15, N=50, j=10, k=10 # but j=k=50 and p=0.5 works well.
# 1/N and i increase responsiveness to hashrate changes at a cost in stability.
# d allows much faster response to *sudden* hashrate changes at a small cost in stability
# target = maxTaget/next_D but use target = 1/D here.
# next_target = 1/D + p*(errorP) + i*avg(errorI) + d*slope(errorD)*N
# use EMA error functions that keep solvetime accurate, e^x =~ 1+x for small x.
# t = ST = solvetime
errorP = (e^(t[-1]/T/N) - 1) * (1-T/t[-1]) * 1/prev_D =~ (t[-1]/T-1)/N/D[-1]
errorI = (e^(tj/T/N) - 1) * (1-T/tj) * 1/Dj =~ (tj/T-1)/N/Dj
errorD = (e^(tk/T/N) - 1) * (1-T/tk) * 1/Dk =~ (tk/T-1)/N/Dk
# where avg() and slope() are for each Dj or Dk and tj or tk over j or k windows.
# Possibly j = k =N is the best setting.
# Notice a slope is "per block" so you multiply N, so the N's cancel.
# update: I set j and k to simple EMA's N=28 and it seems to work at least as well (0.5, -0.2, 0.2)
# D[-1]=difficulty most recent block, T=target solvetime, t[-1] = most recent solvetime.
# When using the approximation, a slight adjustment like 0.99 to the T value in
# errorP is needed to get a more perfect solvetime.
N in the PID2 title is really N/2.3 = 50.

This has the most capability because you can fine tune how it responds. But it's not absolutely clear that it is generally better than the LWMA (LWMA) and Simple EMA.
PID controllers make an adjustment to a variable to achieve a desired goal based on an error signal that is the difference between where the system is and where we want it to be. The "P" of PID means it adjusts partly for the present error. The "I" means we adjust for the recent past average of the error (Integrative part). The "D" part means we use the slope (Derivative) to estimate the future based on the recent slope. Each part has a scaling factor that is tuned to get the desired results. They are then summed to determine the adjustment to the previous setting.
Let
p0 = previous value
p1 = current value
e = p1 - p0 = error signal
a = alpha
D = difficulty
T = target solvetime
t = actual solvetime(s)
1/N = mean lifetime (which is 1/ln(2)*half-life) aka extinction coefficient.
To make a PID controller for difficulty algorithms (see image of book way below), start with the basic EMA equation
ema = a*p1+(1-a)*p0
and rearrange to get
ema = p0+a*(p1-p0).
Although p1 might be our most recent reading, p0 was a forecast of what we expected it to be. Then p1-p0 is the error between our forecast and the actual value. We're adding an "alpha" fraction of that error to our previous forecast to get the next forecast. But we could also add a factor for the recent rate of change of the error in case it's getting bigger. We can add a 3rd factor if we see a recent history of our estimate underestimating the average error. This would then be a standard PID controller:
ema = p0+a1*e+a2*avg(ei)+a3*slope(ej)
where
a1, a2, a3 = the P-I-D constants
ei and ej are over some range i and j in the past
avg(ei) = sum(ei)/i = integral part of PID controller
BEGIN Old Method of Using Difficulty (can be ignored)
Jacob Eliosoff deduced difficulty algorithms need (D=most recent D, t=ST=solvetime):
a=1-e^(-t/T/N), p0=D, p1=D*T/t
which gives great performance and near-perfect solvetimes under all conditions when used as:
Jacob Eliosoff's EMA difficulty algorithm
next_D = D*(1 + a*(T/t - 1))
a=1-e^(-t/T/N)
Plugging this in to the full PID equation gives
next_D = D+a1*error + a2*avg(error_j) + a3*slope(error_k)
However, after much work in carefully defining these constants and errors in order to get them to work (and it worked well), I remembered I had promised myself to NEVER work in terms of difficulty, but ALWAYS in target. This is apparently because solvetimes vary a lot and are in the denominator of difficulty versions, causing problems. I originally desires to work in difficulty because it is proportional to energy (hashes) and I have no grander idea of why a 1/energy like target should be better.
The tortuous way I got difficulty to work for the 2nd term was like this. It uses an avg of ST's to reduce the effect of their variations, which is not required in the target method.
a2 = i*(1-e^(-avg(ST)/T/N))
avg() = avg(D)*( T/avg(ST) - 1)
END Old Method of Using Difficulty
So, due to the problems with difficulty method, instead of using Jacob Eliosoff's original EMA, I used my reverse-engineered version of Tom Harding's simple EMA to get something like Jacob's EMA which is apparently the most ideal EMA because it's the only one that can derive an ideal PID controller in a simple way. Jumping back to beginning of derivation:
ema = p0+a*(p1-p0) (in form needed to apply what the book said)
Defining what my EMA uses: (pT=previous target, T=target solvetime, t=ST=actual solvetime)
a=1-e^(+t/T/N), p0=pT, p1=pT*T/t
Just to show how this is used in a difficulty algorithm:
An EMA for target
next_target = pT*(1+a*(T/t - 1))
a=1-e^(+t/T/N)
Now show full PID controller for target (review what the beginning of this article said on why N is used like this)
PID controller for targets
( BTW next_D = maxTarget / next_Target )
PID next_Target = pT + p*prev_Error + i*avg(Errors) + d*slope(Errors)*N
Errors = (e^(t[j]/T/N) - 1) * (1-T/t[j]) * target[j] =~ (t[j]/T-1)/N*target[j]
j = 1 to k blocks into the past where k can differ from N, but k=N may be best
p=0.5, i = -0.2, d=0.2 (these are decent settings)
The simplified error is based on e^x =~ 1+x for small x, which is applicable for k>10 (20?).
Standard EMA is with p=1, i=0, and d=0, so that's the starting point. The main benefit seems to come from decreasing i below zero and make d larger than zero.
End derivation.
Selecting p, i, and d for speed without harming stability
When comparing algorithms, their N's should first be adjusted to respond equally fast to step functions that simulate what live coins experience. I normalize all algorithms to the same response speed because they can all be made faster by decreasing N. The best algorithm is the one that rises as fast as the others while having the lowest standard deviation. More accidental variation causes more "hash attacks" which also causes more delays. I've compared all the previous algorithms here. After finding the best algorithm, the best value for N is chosen in order to minimize the function ~c/N^0.66 + d*N where c and d are determined by the performance of existing coins.
The following charts show example settings. The first group demonstrates they respond equally fast. [edit:
The PID response does not look as good and shows I made a mistake in the required normalization. Excuse: The metric came out as good and I was not looking at the charts. It looks like the steps were not far enough apart to let it drop back to zero, so it had a head start on the others in rising. ] The second groups shows this algorithm has the best stability during constant hashrate (Std Dev is printed on each chart). The third group is the most important. Those chart show how they responds to simulated miner profit motive, as defined in their titles. [edit: because of the error in the first step, the 2nd and 3rd chart benefits are overstated. The others could have had the same metric with a larger N. However, all of them would have had longer individual attacks and delays. The metric would come out the same because they would have had fewer attacks and delays. This shows the benefit of the PID: you can tune it to give twice as many delays that are 1/2 as bad which may be better than less frequent but longer delays. ]
The metrics are:
% delays = % blocks part of an avg of 11 who's solvetimes were > 2xT
and
"blocks stolen" = number of blocks where hashrate was > 2x what the difficulty was set for.
Low values of these correspond to a lower Std Dev. The charts are ranked best to worst. The values may differ for the given run.
It has thinner red bars in the last group of charts which shows miners will not be able to get "cheap blocks" for long before needing to switch coins. It has 3x fewer delays than Digishield (Zcash) while issuing fewer cheap blocks. But it seems the algorithms are comparable. The SMA is the only one clearly behind.
NOTE: The N for the PID and EMA are 2.3x higher than the N in the equations above so that the EMA responds at the same speed as the LWMA for a given N. Wherever N occurs in the math above, I use N/2.3.
These algorithms are described here.
Why PIDs are marginally useful for difficulty
The reason PID controllers are not better here is because they're meant for systems that have inertia of some kind, like a mass on a spring that gets disturbed away from a desired set point. Since hashrate usually jumps 2x to 3x in a few blocks when difficulty drops 25% below target on accident, there's no mass on a spring here. We have something like a tangent function because hashrate can drop down to zero if difficulty/price ratio gets too high, and up to basically infinity for small coins if it gets too low. Something like the tangent function describes miner motivation which is ultimately the variable we want to control. A tangent function is a difficult mathematical starting point if you want to design a controller. It would not be a PID controller. I wouldn't be able to tune parameters based on the normal methods. The algorithm does not have access to the coin's current price which would be a valuable metric for helping to set difficulty. Unlike other processes, the thing being controlled can see and think about the controller's logic and change its behavior, throwing off any exploitable assumption the controller made.
next_D = 1/ [ 1/D+p/N*(1/D*(t/T-1)) + i/N*avg(1/Dj*(tj/T-1) + d*slope(1/Dk*(tk/T-1) ]
where p, i, and d are the -1 to 1 parameters for tuning it and j and k are the size of the windows for avg() and slope()
Now I can use this to write an accurate algorithm:
( I have not run this code. The testing above was only in spreadsheet )
# PID difficulty algorithm
# Based on next_D = 1 / [1/prevD + P*prevError + I*avgErrors + D*slopeErrors ]
# see https://github.com/zawy12/difficulty-algorithms/issues/20
# Set parameters
# Controller weighting factors (not the ideal ones because this algo is different from testing)
P=1, I=-0.15, D= 0.15
# (P)roportional slowness
N=50 # (same as N = 2.3*50 = 115 in testing spreadsheet)
# (I)ntegration sampling width to calculate recent avg of Error
Ni = 12
# (D)erivative sampling width for to calculate recent slope of Error
Nd = 12
# integrate recent past alpha*error, using e^x = 1+x approximation
for (c=-Ni; c<0 ; c++) {
ST = min((6+1)*T, max(-(6-1)*T,TS[c]-TS[c-1] ))
avgAlphaError += 1/D[c]*(ST/T - 1)/Ni
}
# get average error per block for later use in calculating least squares slope of the alpha*error
for (c=-Nd; c<0 ; c++) {
ST = min((6+1)*T, max(-(6-1)*T, TS[c]-TS[c-1] ))
avgSlopeNumeratorAlphaError +=1/D[c]*(ST/T-1)/Nd
}
# calculate least squares slope of the alpha*error
avgNd = (Nd+1)/2
for (c=-Nd; c<0 ; c++) {
i++
ST = min((6+1)*T, max(-(6-1)*T, TS[c]-TS[c-1] ))
error = 1/D[c]*(ST/T-1)
slopeNumerator += (i-avgNd)*(error-avgSlopeNumeratorAlphaError)
slopeDenominator += (i-avgNd)^2
}
slopeAlphaError = slopeNumerator/slopeDenominator
ST = min((6+1)*T, max(-(6-1)*T, TS[-1]-TS[-2] ))
previousAlphaError = 1/D[-1]*(ST/T-1)
next_D = 1/(1/D[-1]+P/N*previousAlphaError+I/N*avgAlphaError+D*slopeAlphaError)
If you would like me to analyze the performance of your difficulty algorithm, email me at [email protected]. If your coin follows bitcoin-cli or monero json, I can probably get the data, otherwise (or preferably) send me 4,000 to 40,000 blocks with the tab delimited data:
<block number> <timestamp eg 1512345678> <difficulty> <coin price>
would be really nice to have for further analysis if you can get it.
Please describe your coin's algorithm in the following language. Ideally, also copy and paste all sections of relevant code together. If you just say "my coin uses X difficulty algorithm" I may not do anything.
It is important to let me know if it uses MTP as the most recent block data.
Digishield v3 example of how to describe your difficulty algorithm
D=difficulty, T=target solvetime, ST = solvetime, TS = timestamp, N=averaging window
sumST = (0.75*N*T + 0.25*sum(N ST delayed 5 blocks)
sumST = (1-0.16)*N*T if sumST > (1-0.16)*N*T
sumST = (1+32)*N*T if sumST < (1+0.32)*N*T
next_D = sum(past N D) * T / sumST
By "vote" in this article I'm referring to "lottery ticket purchases".
This shows how Nakamoto consensus can be viewed within the framework of classical BFT consensus proofs. In short, each hash performed by miners in Nakamoto consensus functions as both a "proof of identity" and a digital signature on blocks that enables 51% of hashing to be honest. "Selfish mining" that enables <50% attacks is only possible if honest miners switch tips before they've seen enough blocks to be sure the other tip has a higher hashrate. A different solution ("Colordag") was published in 2022 by reducing rewards after-the-fact if splits occur.
A novel aspect of Nakamoto consensus is that instead of requiring synchronization (timed rounds) to count votes, it uses time itself to count votes. Faster blocks means more valid voters (hashes) were participating, but instead of requiring a message from every voter, it assumes silence means failure of a hash to self-identify as the leader. Each silent hash is saying via silence to everyone "no, I am not the leader". The speed of blocks is proportional to the participating failures ("proportional" only when averaged over at least a few blocks due to exponential & Poisson distributions, with Erlang distribution N/(N-1) error).
To summarize, I conceptualize Nakamoto consensus as having 2 remarkable aspects that made it seem to violate old consensus proofs:
This is background work to support reverse Nakamoto consensus which shows how to replace POW's hashrate with a POS-VDF stake-rate. This is done by 1) using a Verified Delay Function to prevent double-voting by giving a time-denominator to stake, and 2) reversing the Nakamoto consensus process because stake is on the chain before elections whereas hashrate proves itself during elections. This prevents the seed to randomization from being tainted by grinding attacks.
In order to get Byzantine fault tolerance (BFT) in distributed consensus with 67% of voters being honest, they're required to have clocks that are synchronized within a known max error in order for all voters to know when voting rounds begin and end. To do it with only 51% of the voters being honest, this synchronization is required as well as authenticating ("digitally signing") votes.[0] There are no known exceptions other than Nakamoto ("POW") consensus variants. How does POW do it? Who are the voters, how do they register, and how do they digitally sign their votes? It's usually treated as somewhat of a mystery or complicated[4][5], or Nakamoto consensus is denigrated by claiming it achieves "only" eventual or probabilistic consensus instead of "Byzantine consensus"[3]. But the probabilistic nature is a feature, not a bug, repairing damage from "temporarily successful" attacks that can't be fixed by any other method. It's not classified as Byzantine consensus or Byzantine agreement by noted authorities[1][2], ostensibly because it achieves Byzantine fault tolerance without seeming to possess the traditional requirements.
"Selfish mining" using < 50% to get blocks works only if miners switch tips when an alternate tip is only 1 to 3 blocks ahead. If honest miners follow a policy of not switching unless the alternate tip is 4 or 5 blocks ahead, a selfish miner would have to have > 45% of the total hashrate. So selfish mining is able to work with <50% only if honest miners are not waiting long enough to be sure the alternate tip has the higher hashrate it claims (no manipulative block withholding). In this way Nakamoto consensus is more synchronous in addition to having digital signatures in order to have nearly 50% protection.
Summary of Nakamoto consensus as a Byzantine consensus
Nakamoto consensus can be viewed as being within "traditional" Byzantine requirements by these substitutions. This shows Nakamoto consensus's success should not be used as evidence the traditional minimal requirements are in error, or that the lack of traditional requirements show that Nakamoto should be distrusted.
Synchronous Voting
The beginning of each voting round in POW is clear to all: it begins when a new tip is received. All potential voters are sync'd to the beginning of the vote within propagation delays. If there is a glitch in the network, some voters will not be present. The end of a voting period is equally clear and "sync'd", but very different from a traditional method in not being a specific time or a specific length of time after the vote began. A measurement of time (node time) is still crucial (as described below) despite not defining "when" the vote begins and ends. As with traditional Byzantine consensus under similar circumstances, "network asynchrony" (propagation delays) must be small compared to the voting period.
Solvetime measures number of "no" votes
The average length (and therefore end point) of a POW voting period changes only when the hashrate changes. The variation in individual solvetimes due to the Poisson distribution for a given hashrate and difficulty is a fixed average. By revealing changes in hashrate, the number of voters (hashes) in the voting period is revealed. A traditional vote has a known number of voters by collecting all the votes and requiring them to vote in a fixed length of time. POW turns this upside down and uses the observed voting time to measure the number of voters. This enables it to use their silence as their "no" vote that says "no, my block hash was not below the target", saving a massive amount of communication. This is POW's most impressive feature. Normally at least two messages per voter are required: one to receive news of the previous winner and one to cast a vote. The best "traditional" Byzantine consensus mechanism that does not use this trick requires 8 rounds of communication.[1] POW does it with a single message (the block) for each voting round that announces the end of the previous round and beginning of the next round, and proves the winning vote was from a valid voter and "digitally signed".
Eventual probabilistic finality is a feature, not a bug
POW results in a chain that probabilistically demonstrates it had a higher sum of contiguous voters (in the face of a partitions) than any other chain, not that it necessarily had >50% of voters. This enables it to resolve network partitions, eventually. "Traditional" Byzantine consensus must also solve network partitions (accidental or malicious) eventually by the same method of waiting for partitions to resolve and many are permanently if they can never get >50% of the votes. This is not an option in BTC. And yet, "eventual consensus" is used like an insult and incorrectly cited as the cause of various problems.[3] Some researchers seem to re-defined Byzantine agreement to exclude "eventual probabilistic consensus" in order to make Nakamoto consensus distinct from the prior 30 years of "traditional" Byzantine consensus, but it is a fictitious division. The real reason for the division seems to be because it is not easy to see that Nakamoto consensus is working within the "traditional" boundaries. The purpose of this article is to show POW does not magically or by any failing circumvent the old proofs of decentralized consensus limits.
Voter registration is during the vote
Nakamoto consensus does away with the usual need for voters to register their identity or even their existence, but that does not mean it is not aware of their number, which is the only thing necessary in a yes/no vote where there is only one voter who will have the "yes" vote. The solvetime measures the number of "no" votes and only the winning "yes" voter needs to reveal himself. The hash has a cost that gives the right to vote, preventing Sybil attacks. "Right to vote" is another way of saying it gives the voter (a hash) an "identity" because cost is inherent to identity. With beautiful efficiency, that cost, which is inherently part of the real world through equipment and an energy expense, is also how a true physics-based randomness is obtained.
Voter identities (hashes) must be produced during the vote based on the previous hash winner. The production and cost of identity-formation during the vote without even knowing who the voters are is fundamental to how it's known these unknown voters exist and are not double-voting during the vote. This aspect is why the value of a stake in POS can't simulate everything a hash does. Both have a demonstrable value that can establish identity. But only when POS is combined with a Verifiable Delay Function (VDF) in a way that prevents double-voting during the vote can it work as well as POW (see my Reverse Nakamoto Consensus article). The centralization of masternodes with stake that is locked up over time is another way to prevent double-voting that deviates from the beauty and efficiency of POW.
[0] Digital signatures being required to enable 51% instead of 67% honest nodes was shown by Lamport et al in section 5 of their 1980 paper "Reaching Agreement in the Presence of Faults" and section 4 of their 1982 paper "The Byzantine Generals Problem". It enables every node to know what every other node voted. Requiring nodes to also synchronize enables every node to "see every vote".
[1] (Abraham et al 2017) Efficient Synchronous Byzantine Consensus
https://eprint.iacr.org/2017/307.pdf
Perhaps somewhat surprisingly, we do not yet have a practical solution for Byzantine consensus in the seemingly easier synchronous and authenticated (i.e., with digital signatures) setting. To the best of our knowledge, the most efficient Byzantine agreement protocol with the optimal f < n/2 fault tolerance in this setting is due to Katz and Koo [21], which requires in expectation 24 rounds of communication (not counting the random leader election subroutine).
[2] (Abraham et al 2016) Solidus: An Incentive-compatible Cryptocurrency Based on Permissionless Byzantine Consensus
See Table 1 that calls their Solidus mechanism "Byzantine" as if it is more like "classical" Byzantine mechanisms than "Nakamoto" consensus, despite also using POW and a permissionless setting. They define Byzantine consensus:
Byzantine consensus is a classical problem in distributed computing in which a fixed set of participants, each with an input value, try to decide on one input value, despite some participants being faulty.
which implies they justify calling their own permissionless POW Byzantine instead of Nakamoto consensus because they use a fixed number of committee members. But Lamport et al's 1980 and 1982 papers do not fundamentally require n to be a constant over more than 1 voting period, and if there is a network partition, an algorithm may accept whatever n it sees, indicating a fixed set of participants is not a valid way to define Byzantine consensus.
[3] (Kokoris-Kogias, 2016) ByzCoin Enhancing Bitcoin Security and Performance with Strong Consistency via Collective Signing
https://www.usenix.org/system/files/conference/usenixsecurity16/sec16_paper_kokoris-kogias.pdf
The 6 references cited in the following are unrelated to probabilistic guarantees, so the assertion is without reference.
Later work revealed additional vulnerabilities [in POW] to transaction reversibility, double-spending, and strategic mining attacks [25, 31, 34, 35, 48, 3]. The key problem is that Bitcoin’s consensus algorithm provides only probabilistic consistency guarantees. Strong consistency could offer cryptocurrencies three important benefits.
They then go on to say existing solutions cause other problems (which are worse in the context of BTC). Their own solution was found unsatisfactory in [2].
[4] (Garay 2019) The Bitcoin Backbone Protocol: Analysis and Applications
https://eprint.iacr.org/2014/765.pdf
However a thorough analysis establishing the exact security properties of the Bitcoin system has yet to appear.
[5] (Pass, Sheman, Shelat, 2016) Analysis of the Blockchain Protocol in Asynchronous Networks
https://eprint.iacr.org/2016/454.pdf
The analysis of the blockchain consensus protocol (a.k.a. Nakamoto consensus) has been a
notoriously difficult task. Prior works that analyze it either make the simplifying assumption
that network channels are fully synchronous (i.e. messages are instantly delivered without delays)
(Garay et al, Eurocrypt’15) or only consider specific attacks (Nakamoto’08; Sampolinsky and
Zohar, FinancialCrypt’15); additionally, as far as we know, none of them deal with players
joining or leaving the protocol.
This one is here for historical purposes. The EMA-Z is preferred over this one because this one can't handle zero solvetimes, requires e^-x calculation, and can't be done with integer math. The WHM is the best one
# Jacob Eliosoff's EMA (exponential moving average) difficulty algorithm
# https://en.wikipedia.org/wiki/Moving_average#Application_to_measuring_computer_performance
# see https://github.com/zawy12/difficulty-algorithms/issues/1 for other algos
# ST = solvetime, T=target solvetime
# height = most recently solved block
# There's a "2" in the exponent below to make the above N comparable to SMA, WT-144, & WWHM
# MTP should not be used
T=<target solvetime>
# Ideal N appears to be N= 40 to 85 for T=600 to 60 by the following formula.
# see https://github.com/zawy12/difficulty-algorithms/issues/14
N=int(50*(600/T)^0.3)
# Choose a limit on on how large solvetimes can be based on keeping
# difficulty from dropping more than 20% per bad timestamp.
# Varies from 5 for N < 50 to 9 for N > 76.
# The way it is used in the code makes it a symmetrical limit.
limit = max(5,min(int(N/0.90)-N,9))
maxT=timestamp[height-limit-1]
for ( i = height - limit to i < height ) { maxT = max(maxT, timestamp[i]) }
ST = timestamp[height] - maxT
ST = max(T/200,min(T*limit, ST))
next_D = previous_D * ( T/ST + e^(-ST*2/T/N) * (1-T/ST) )
This is probably better than 95% of all difficulty algorithms currently in use. This has half as many delays and blocks lost to big miners as Digishield. It's a few steps above a simple moving average. See EMA-Z for full discussion of EMA math.
Email me at [email protected] before you go to testnet to show me your code. If you have a public api send me link to it so that it can be included in the Difficulty Watch page.
Cryptonote coin need to apply the Jagerman MTP Patch You can read his summary of it here and full background and description is here. All Cryptonote coins need to do this ASAP. It does not require a fork.
Cryptonote coins might use the following (I'll edit this later after someone has told me it works or fails in testnet):
// Simple EMA difficulty
// Copyright (c) 2018 Zawy
// https://github.com/zawy12/difficulty-algorithms/issues/21
// N=28 chosen to be same speed as LWMA N=60 and 30% faster than Digishield
// EMA math by Jacob Eliosoff and Tom Harding
// const uint64_t CRYPTONOTE_BLOCK_FUTURE_TIME_LIMIT = 3xT; // (360 for T=120 seconds)
// const size_t BLOCKCHAIN_TIMESTAMP_CHECK_WINDOW = 11;
// const size_t DIFFICULTY_WINDOW = 28+1;
// Difficulty must be > 100 and < 1E13.
difficulty_type next_difficulty(std::vector<std::uint64_t> timestamps,
std::vector<difficulty_type> cumulative_difficulties) {
// For readability and portability, clone vectors
vector<T> TS(timestamps);
vector<T> CD(cumulative_difficulties);
// Startup
uint64_t initial_difficulty_guess = 100;
if ( timestamps.size() < 2 ) { return initial_difficulty_guess; }
// Suggestion for forks if new hash rate < 1/10 of old hash rate.
// if (height < fork_height +2 ) { return initial_difficulty_guess; }
// ST must be signed.
int64_t N = DIFFICULTY_WINDOW - 1;
int64_t T = DIFFICULTY_TARGET*0.982; // seconds
// The following cast results in a disaster after fork if done with doubles
int64_t ST = static_cast<int64_t>(TS.back()) - static_cast<int64_t>(TS[TS.size()-2]) ;
int64_t D = CD.back() - CD[CD.size()-2];
// Limit allowable solvetimes to help prevent oscillations and manipulations.
ST = std::max( -5*T, std::min( ST, 6*T));
// Do the magic.
int64_t next_D = (D*N*T)/(N*T-T+ST);
return static_cast<uint64_t>(next_D);
}
Just out of mathematical interest, re-arranging Digishield's math gives:
next_D = avg(17 D) * 4 / ( 3 + avg(17 ST)/T)
The simplified EMA with a similar speed of response is
next_D = prev_D * 36 / ( 35 + prev_ST/T)
CN forks very often (if not always) result in constant chain splits due to different difficulties. It's either because the new code is not backwards compatible with the old code in how old difficulties were calculated AND nodes popped blocks back to different points, AND/OR nodes just have different code that's not completely incompatible. Once a node has different difficulties in their local database due to one of these things, they will never have the same difficulties in the future. If it gets 10% too higher, it will always be 10% too high even if the code (that recreated the database after that point) is the same. Nodes with a lower difficulty will have a certain percentage of "their" miners' blocks rejected by nodes with higher difficulties, but they will accept all the blocks from the miners with the higher-difficulty nodes. If the lower-difficulty chain pulls ahead from having more miners, the higher difficulty nodes stay on a branch, never accepting the chain with the highest work due to rejecting its blocks. Miners may remain unknowingly married to those nodes on a chain that looks profitable without realizing their blocks have been orphaned. If the higher-difficulty chain pulls ahead, miners with the lower difficulty nodes will have some of their blocks rejected without realizing why.
New code must calculate the old difficulties in the exact same way in order for the new difficulty algorithm to get the correct beginning input difficulties. Otherwise different sync heights will create different chains or mass confusion from different difficulties on the same chain. There's no repair except to find the backwards incompatibility, fix it, and re-fork at the same height, or manually force the N difficulties before the fork to the correct values (an ugly solution). The last test of your fork is to make sure your new difficulties when you sync from 0 are matching the old difficulties when running the pre-fork code. If the last difficulty before the fork is the same in both, then almost assuredly every difficulty before it will be correct.
But there is a way to prevent, stop, and/or cover up the problems and get everyone with the same difficulties, as long as they have the new code and pop blocks back to at least 1 block before the fork. The new code does not have to be backwards compatible and you don't have to create a new difficulty algorithm. I've incorporated this into my difficulty algorithms. You simply put this in the algorithm:
uint64_t difficulty_guess = 100000; // Dev changes. Guess a little lower than expected.
if ( height >= fork_height && height <= fork_height + 1 + N) {return difficulty_guess;}
Where "N" is the number of blocks used in the difficulty algorithm. This forces all the difficulties to be the same no matter what was in the database prior to the fork. This does not resolve all the problems because some nodes will not upgrade their code.
As an example of backwards incompatibility, the following single change caused a lot of problems in Lethean's 269000ish fork. They were lucky a roll back to the fork height was not required. A roll back was not needed bbecause most miners were working on a chain that was not resync'd from zero, and the only wrong difficulties were way back in time to the previous fork, so the correction enabled those who resync'd from 0 to get the same difficulties.
Post a comment to this issue if we say anything important CN / Monero clones need to know. Edit your previous comment instead of adding more than 1 comment per person. I'll start.
There were some discussions yesterday about merged-mining and how to stop the capability. We are running a fork of TurtleCoin and wondering if you guys ever came up with a good solution we could start testing...?
Just do a hard fork to a new block template with no TX_Extra
This keeps a really smooth difficulty by defaulting to a large N, but switches to a smaller N if there is a sudden >3x increase or <1/3 decrease in hashrate. It may be that the basic EMA with N=70 is generally just as good for all coins. N here is in a e^(-2/N) formula instead of e^(-1/N).
# Dynamic EMA difficulty algo (Jacob Eliosoff's EMA and Zawy's adjustable window).
# Bitcoin cash dev(?) came up with the median of three to reduce timestamp errors.
# "Dynamic" means it triggers to a faster-responding value for N if a substantial change in hashrate
# is detected. It increases from that event back to Nmax
Nmax=140 # max EMA window
Nmin=50 # min EMA window
A=11, B=2.1, C=0.36 # A,B,C = 11,2.1,0.36 or 20, 1.65 0.45,
# TS=timestamp, T=target solvetime, i.e. 600 seconds
# Find the most recent unusual event in the past 20 blocks event
for (i=height-Nmax; i < height; i++) { # height - 1 = most recently solved block
if ( (median(TS[i],TS[i-1],TS[i-2]) - median(TS[i-A],TS[i-A-1],TS[i-A-2]))/T/A > B
or
(median(TS[i],TS[i-1],TS[i-2]) - median(TS[i-A],TS[i-A-1],TS[i-A-2]))/T/A < C )
{ unusual_event= i-height+1+Nmin }
}
N = min(Nmax, unusual_event))
# now do the EMA-Z with this N. See link below:
See EMA-Z algorithm for the rest of the algorithm.
Another dynamic window idea I want to test and specify here triggers on a more advanced and more responsive rule. The above has a problem: it needs 20 blocks out of fear of timestamp manipulation. The statistical check could be more precise and flexible. I'm thinking along the lines of:
For past i= 3 to N/2 blocks, check if the sumST of each "i" is above or below the (say) 1% level of expectation. It has to be done carefully. For example, getting only 3 when we expect 10 occurs 1% of time. "Out of the time" means per group of 10 blocks. How does a rolling check on this figure into it if the 10 should be a random selection? But it appears it would be triggered 1 per 1000 blocks. Let's jump ahead to i=7 and I see this few may occur in 16xT at the 1% level...but it's in 16xT blocks, so it occurs 1 per 1600. To get 1 in 1000 again, I need i=7 or less in time 15.3xT. It looks like a lot of work and trial and error to get the constants for each "i", but it might work a lot better than the above.
I made this article long and complicated, so let me try to summarize "how to identify the best algorithm":
Normalize their "N" parameter until they all have the same response to 2x to 5x attacks that last from 10 to 30 blocks (very typical of what Zcash and other coins see). I average the values they have at the end of the step function to make sure it is about the same value. Any of them can be faster or slower based on the N. Speed comes at a price of stability. You get speed proportional to 1/N and stability with SQRT(N). Then, to check overall performance, I model real attacks that being when difficulty is 0.7 to 0.95 of the baseline difficulty. The attacks can be 2x to 25x hashrate which occurs in small coins. The attack lasts until the difficulty reaches 1.1 to 5x the baseline difficulty. I have metrics that measure delays and "blocks stolen at low difficulty", which ranks the results. This turns out to be the same as the winning algo having the lowest root-mean-square of the error between where the difficulty should be based on the hash rate and where the difficulty is. And for a given speed of response, the winner can be identified apparently just as well by just choosing the one with the lowest standard deviation when the hash rate is constant (since it drops lower less often, it will attract fewer hash attacks and therefore score better).
The reverse process for objectively determining the best algorithm can be used: Adjust their N parameter until the competing algorithms have the same StdDev when the hash rate is constant. The one with the fastest response to the "hash attacks" you expect is the winner, which is LWMA with Digishield again tying for 2nd place with EMA and clearly beating SMAs. The reason SMA is not good is because it is getting the avg hashrate as it was N/2 blocks in the past, while EMA and LWMA are estimating current HR. Digishield is not quite as good because it's tempering it's calculation of 17/2 blocks in the past, but a lot better than SMA because an equivalent-speed SMA is N = 4x17 = 68 which is 34 block behind.
This is complicated, but necessarily so.
The biggest problem in identifying the best algorithm is first defining the metric for success. I define it as "the least random variation at a constant hashrate for a given speed of response". "For a given" refers to competing algorithms having a parameter "N" that can be decreased to meet the speed requirement which causes a loss in the stability requirement. A related article to this is the Selecting N article which tries to identify the ideal N to make this balance, once you've identified the best algorithm.
I've checked this method against other methods such as having the fewest 2x target solvetime delays and having the lowest sum of squares error when miner profit motivation is simulated. For those interested in the "least squares" error measurement, I believe we should use:
if ( nD/D > 1 ) { (1-nD/D)^2 } else {(1-D/nD)^2 } where nD=needed difficulty for the given hashrate
instead of the standard (nD-D)^2.
This is for each block where D is what the algorithm generates. Then sum these up and take the SQRT to scale it down. This is an RMS of the error where error is defined in a way that meets our needs.
To repeat, all algorithms have a parameter "N" that increases stability at the expense of its speed of response as you raise the N. When comparing algorithms, the best thing to do is first find their "equivalent ideal N" by checking their response to a sudden increase in hashrate. ( BTW All acceptable algorithms will be symmetrical (equal) in their increase and decrease rate to sudden changes or the target solvetime will average too high (or too low) and oscillations will be present. If your target solvetime is too low, then your algorithm is decreasing faster than it increases. )
To find the equivalent N, you send the algos step functions in hashrate that are some multiple of baseline hashrate and a fixed width apart, and make the steps 2x that far apart for the difficulty to drop back to normal. Their equivalent N will change a little bit for different step functions, so your step function should model the kind of ability you want the algorithms to have. I use 2x to 3x hashrate step function and select a width where the algos have reached about half-way to where they should be for that hashrate (about N/2 for the N of the current champion algo). You average D for the last block at the end of the all the step function "assaults, needing 10,000 block runs to get 100 data points for steps that are 33 blocks wide with 66 block gaps.
For a given N in an SMA, the equivalent speed of response in the other algorithms with step functions N/2 wide are:
WHM = WT = 1.32xN
EMA = 3.3xN using e^(-t/T/N) instead of my e^(-2.5*t/T/N)
Digishield = N/4.25
For wider step functions, SMA needs a larger relative N, and vice versa. But thankfully the relative N's for the others stay closer for different width step functions because they are faster in starting a correction.
After their "equivalent N" is found to standardize the speed of response you want to the type of hash rate changes you expect, you then check their stability during constant hashrate (not during hash rate changes where you want high variation). The algorithm with the lowest standard deviation of the difficulty wins. If you want to increase stability, you have to increase N which will sacrifice the speed you wanted. You would change the equivalent N for the competing algorithms by the same percentage to keep them all in the same terms.
In order of the best algorithms, the standard deviations for the WHM N=60 (which I think is the best for coins with target solvetime T=150) are:
WHM = 0.13
EMA = WT = 0.14
Digishield = 0.15
SMA = 0.16
This seems small but the difference between SMA and WHM is about 3x fewer delays and 20% fewer hash attacks. My charts below are for WHM with N=90 (and the others with their equivalent N).
You will find that all algorithms have too much instability for the speed of response you want. To balance the competing goals to make the best of a bad situation, see the Selecting N article.
If the above process is confusing or suspect, my old method is a good check and it's shown in the last chart below. It's done like this this: The equivalent N as before is found and used. Instead of simply looking as Std Dev, I subject the algos to expected miner profit motivation. Miners want the lowest Price/Difficulty and view a 20% increase in price the same as a 20% decrease in difficulty (or more precisely 1/1.20 = 0833 => 16.66% decrease in difficulty). So the simulation says "during constant hashrate conditions, if difficulty drops below A% of the correct difficulty then a Bx the baseline hashrate "attack" begins, and ends when the difficulty is C% above the correct difficulty. If an algo varies a lot, it gets attacked a lot, but if it varies a lot it is also responding quickly to have fewer blocks "stolen" in each attack. so it's a complex feedback situation that needs test runs and measurement....but it's all simplified because I've already standardized the number of blocks stolen in each attack by standardizing the response speed. This is why all the red bars in last chart are approximately the same width. To be more accurate I comparison, if my miner motivation is correctly modeled, then N should be refined to make the red bars in all algos of equal width, but the further refinement is not important because of a "can't win for losing" effect from the "complex feedback situation". For example, Digishield seems cheated because it has a faster-than expected response (thinner bars) in comparison to how I found its equivalent N. If I increase it's N, then the delay metric gets even worse and that's its main problem compared to the others.
The DWHM-EMA is not easily expressed in terms of the others, but it seems to be the best algorithm. It's not published yet due to complications that make me think it's all the same as WHM and because I already have its cousin published, the Dynamic EMA.
In the charts below, the "delay" and "blocks stolen" percentages are the number of blocks who's average of 11 solvetimes were > 2x target solvetime (delays) or < 1/2 target solvetime ( the difficulty is set too low for the amount of hashing). These are the check on the Std Dev conclusion The number in the charts vary for different runs. I've sorted the charts from best to worst based on more data.
The following ranking is based on 8x delay percentage plus the "blocks stolen" percentage.
WHM-EMA 15.6
WHM 18.3
EMA 20.5
WT 25.4
Digishield 27.9
SMA 36.4
My current estimate of the best N based on the target solvetime for LWMA is:
T = 600, N=45
T = 300, N=55
T = 150, N=70
T = 75, N=85
Medium size coins and coins who are confident their POW will not be subject to on-off mining like NiceHash should double these numbers. The largest coins should triple these numbers. The choice is a balance between wanting a fast speed of response by lower N to keep up with network hashrate changes and not wanting random variation caused by lower N to encourage hashrate changes. For example, BTG with N=45 and T=600 will see a typical random variation of 1/SQRT(45) = 15% every 45 blocks, which is 7.4 hours. 15% is probably 5x more than the typical price+fee changes they will see every 7.5 hours, so I've probably recommended a value too low for them because with their unique equihash POW, they would probably not see 5x or 10x changes in hashrate 5x per day, which is what the N=45 would try to protect.
The above 45 should be changed to 10 for if you're using my termpered SMA (like digishield). For SMA make it 34. For EMA make it 20. This will give all 4 algorithms the same speed of response to a hash attack that is 3x to 30x your baseline hashrate after about 20 blocks. They differ in how soon they rise after an attack begins (some start slow like SMA but then catch up and pass others that were initially ahead like Digishield) while other are more stable, but have more post-attack delays (digishield verses EMA).
More recent comment from me:
Q: "What should N be for T=300?"
A: "N=50 to 60. I have no solid ground or intuition for choosing N, except that it should be in the N=45 to N=90 range for T=240 or thereabouts. A coin that is the largest for a gven POW might use N=200 to have a really smooth difficulty with little ill effect. So for the typical micro to small coins we have, I say N = 50 might be good, but sticking N=60 makes it more comparable to existing LWMA's. and LWMA-2 may completely change this......maybe all N's need to rise 50% to 100% now that it can rise so fast.
But I would say just stick with N=60."
Introduction / background
The choice of N for the size of an averaging window in a difficulty algorithm is more important than the algorithm (if the algorithm is at least as good as a simple moving average).
Choosing N tries to achieve a balance between a fast response to price (and other causes of hash rate changes) and minimizing accidental variation that accidentally attracts or discourages hashrate with an incorrect difficulty. Smaller N gives faster response but higher variation. The speed at which the difficulty can keep up with price changes is proportional to N*T. The accidental variation in D in block time is proportional to 1/SQRT(N). Approximately, we want to minimize some function like this:
A/SQRT(N) + B*N*T
i.e.: variation + slowness
where A and B are some unknown scaling factors that relate the relative importance of 1/SQRT(N) and N*T. It needs to be determined by watching the results of a lot of live coins. The left side does not contain time, but it should because the number of instances of variation in real time depend on T. But deciding how to include it is complicated as shown further below. My estimate is that it's a 1/x^0.33 function instead of 1/x^0.5 near the optimal points, and degrades to 1/x as too much variation starts becoming really attractive to opportunistic miners.
So stability increases as 1/N^0.33 while speed decreases linearly with N, so there's a mathematical advantage to be biased towards a low N. But if the stability causes the variation to go above about +/- 20% of the correct difficulty, droves of miners will suddenly be coming online and offline whenever that event occurs, amplifying instability (but not necessarily causing bad oscillations: some coins are satisfied with N=17). On the other hand, if it's responding fast enough, fewer miners are going to bother switching coins to "attack" the accidentally low hashrate. The chart below estimates the effect I see in live coin delays and hash attacks. I had to use 1/N^0.66 to get the left side of the curve.
It appears very likely that a specific N can be chosen to be good all reasonable target solvetimes (60 to 600). There's a plateau in the above graph that suggests this.
Miners seek best price/difficulty ratio. If the price/difficulty ratio drops by 25%, there is typically a 300% increase in hashrate (in the coins I follow) until the difficulty catches up. So we want to respond fast enough to keep up with price changes, but we don't want to accidentally go 25% too low because to a miner that's the same thing as a 25% price increase.
BTW if the price and hash rate of a coin changed in "block time" instead of "real time", then changing T would have no effect on the difficulty algorithm's math or performance.
Live coins with different N and T values
If the above gives an accurate idea of how we should change N relative to T, then we still need a good starting point as determined by watching live coins.
N=320 is definitely too large for coins with T=240 seconds (target solvetime) as seen in Monero clones. BCH's N=144 with T=600 is not performing as well as other coins in terms of delays. Zcash clones with T=150 seconds are doing pretty darn good with Digishield v3 and could do better if they employ my modifications to it. Digishield v3 with N=17 is like an N=60 algorithm. Two or four times a day both Zcash and Hush see a 3x increase in hashrate for 20 blocks. Masari with T=120 and N=60 my WHM is doing the best of the 7 difficulties I follow. Compared to Zcash and Hush, it gets 1/2 as many of these "hash attacks" per day ("attack" = avg 11 solvetimes < 1/3 T) and 1/3 as many delays (delay = avg of 11 solvetimes > 2xT).
720 x 120 and 300 x 240 = disaster (Karbowanek, Masari, Sumokoin, et al)
144 x 600 = not very good (BCH)
60ish x 150 = pretty good (Zash, HUSH)
60 x 120 = super awesome (Masari)
17 x 600 = not bad (if BTG's had not been screwed by bad POW limits)
17 x 240 = fairly bad (Sumokoin, Karbowanec)
17 x 120 = disastrous (Masari)
A good algo seems to have about N=60 and T=150 which will have a 25% change in difficulty from random variation once every day, but price does not typically change near that much. So there seems to be a strong bias towards keeping a faster response than price change alone requires. Maybe it's partly because 10% to 15% of hash power can come and go even with a constant price/difficulty ratio and it's good for the algorithm to respond quickly to those changes, especially if they coincide with a 10% change in price a couple of times per week. But a bigger reason we seem to need algos with more accidental variation is that they are able to correct themselves quicker, so the higher variability is not so harmful.
Changing N when T changes
Once we know the ideal N and T for a particular algorithm, we should choose a larger N for a coin that has a smaller T, and vice versa. Since there are more sample points in real time for a smaller T, we can have a better functioning algorithm. With a smaller T we can choose a faster response, less random variation, or a smaller improvement in both.
Options if T is made smaller: (N will be larger)
Less random variation in real time, same response rate:
new_N = old_N x old_T / new_T
where T=target solvetime.
Faster response in real time, but same random variation in real time
new_N = old_N x (old_T / new_T)^0.33
(see footnote on the source of 0.33)
A little bit better response rate and a little less random variation
new_N = old_N x (old_T / new_T)^0.66
This gives N=1.5x higher when T is 1/2.
Options if T is made larger (N will need to be smaller)
Use the same equations above, but replace "less", "faster", and "better" with "more", slower", and "worse". Larger T means fewer data points per day to estimate the network hashrate, so the algorithm is necessarily not going to be as good.
Foot note:
Source of my 0.33 above:
For a given algorithm and level of probability, difficulty randomly varies as +/- k*StdDev/SQRT(N) in every group of N blocks. k is a constant that depends on the algorithm and on the value of standard deviation. StdDev=1.96 means 95% of difficulty values will be within that range. k is about 1.1 to 1.6 depending on StdDev and the algorithm. It's not precise because D is not a Gaussian random variable even if hash rate is constant. I'll assume k=1 here because I'm looking for a trend that will give me a power factor, not a precise result (because I don't know A and B anyway).
Let's assume I want to keep random variation down to one 25% accident every 5 days because I do not expect price variation to be more than that, and I sort of want the two variations about equal in an effort to balance them (this is like assuming A=B=1, but I believe A<B). There will be 5 x 24 x 3600 / (NxT) sets of N blocks. For a single set, a 25% variation will approximately obey the equation:
0.25 = StdDev/SQRT(N)
I want an N that has a 25% variation in difficulty in 5 days when the hash rate is constant.
With T=600, there are 5 days x 24 x 3600 / (Nx600) = 720/ N sets of N blocks. I will first guess the ideal N is 60, so there will be 720/60 = 12 sets of N blocks in 5 days. I want a 1/12 chance of having a 25% variation in each set of N blocks. A chart tells me a 1/12 two tailed probability has a StdDev of 1.53. Now I solve:
0.25 = 1.53/SQRT(N) => N=37
The true N I seek is about half way between my N=60 guess and the N=37. I try again with (37+60) /2 = 49. 49/720 = 6.8%. Chart gives StdDev =1.83 for 6.8%.
0.25 = 1.83/SQRT(N) => N=54
So it seems N=(49+54)/2 = 52 is a pretty good choice for T=600 and 25% variation once in 5 days.
Repeating the same process for T=300 and T=150 gives N=64 and 78. These number follow the trend
N=52*(600/T)^0.31
Repeated for a different set of conditions gave a power of 0.33.
This discusses an accuracy error in fixed-window difficulty algorithms that was brought to my attention by Pieter Wuille's twitter poll and result. Meni Rosenfeld wrote a paper about it in 2016. It also shows how coins and pools are not calculating hashrate precisely correct. It makes a big difference if you're estimating hashrate with a small sample.
Large error due to not taking increasing hashrate into account
BTC difficulty adjustment have historically been almost a day before the scheduled 2 week target adjustment (coin emission is now about 7 months ahead of time) because hashrate usually increases (an average of about 6% per two weeks) before the next adjustment is made, so emission has been 6% faster every two weeks. This could have been corrected by looking at the past 4 weeks and adding on an adjustment for the slope, thereby taking into account the "acceleration" in hashrate instead of just its most recent "velocity".
Commonly known 2015/2016 error
It is well-known that without the above "ramp error", the BTC code has an error that would have caused the 2016 block adjustment to take 2 weeks and 10 minutes. This comes from the code being like this:
next_target = previous_target * sum_2015_solvetimes / target_time_2016_times_600
This is the same as:
next_target = previous_target * avg(2015 solvetimes) / 600 * 2015/2016
This 2015/2016 is the cause of the lower-than-intended target (higher difficulty).
There is another 10 minute error in the same direction as BTC's known code error. It applies to fixed-window difficulty algorithms. The error is a lot smaller in simple moving averages. I can't figure out how to analytically determine the adjustment in simple moving averages, but the correction I've experimentally determined to be accurate down to N=4 is adjusted target = target/(1-3/N^2).
Satoshi and pretty everyone else thought for years that the next target (~1/difficulty) should be determined by:
T = desired block time
t = observed solvetimes
HR = hashrate
nextTarget = priorTarget * avg(t) / T = 2^256/(T*HR)
The above basis of all existing difficulty algorithms is wrong because in estimating HR to adjust the target, you have N samples of previous solvetimes (t) but the probability of fast solvetimes is higher (which is offset in an N=infinite average by some solvetimes being substantially longer). So when you take a smallish sample N of them, you're more likely than not to have more fast blocks. This causes the difficulty calculation to overestimate the hashrate and thereby set the target too low (difficulty too high) which makes the resulting avg solvetime higher than your goal.
The correction turns out to be simple, which appears to be directly related to the memoryless property (see bottom section "Similar Effect"):
nextD = nextD * (N-1)/N
nextTarget = nextTarget * N/(N-1)
I tested it all the way down to N=2 with no discernible error. It has a problem at N=1.
Derivations
My derivation below is based on what I needed to understand it. Others have a much more efficient way to explain it in a language I don't grasp. Meni Rosenfeld's paper derives it. Pieter Wuille did a poll and has an explanation. Pieter says it comes from
E(1/X) where X~ErlangDistribution(N,1)
Code to prove the error
Here is code Pieter did to show the error is occurring in BTC. Note line 34 is the sum of the past 2015 solvetimes that skips the first solvetime in the 2016-blocks of solvetimes in the array, just like BTC, so the avg solvetime will shows the both the old and new error combined: 600*2016/2015*2015/(2015-1) = 600.6 seconds.
https://gist.github.com/sipa/0523b510fcb7576511f0f670e0c6c0a5
A Similarly Unexpected Effect
The above N/(N-1) adjustment seems to be related to a surprising fact that 91% of Pieter Wuille's followers missed. Given a mean time to occurrence of T = 1/λ, when you take a random sample of time 2*T you see on average only 1 occurrence. Another way to say it is that if you take a random point in time, it will be T to the next block by the memory-less property. But memory-less is history-less and therefore works backwards in time as well so the time to the previous block is also T. Another way to say it is that some solvetimes are long enough to offset the more frequent short solvetimes, so random samples often fall somewhere inside a long solvetime. See also Russel O'Conner's article. This is extendable to longer periods of time. If you take a random sample of time that is N*T then you will see on average only N-1 blocks.
T = average solvetime = 1/λ
average(N blocktimes) = T
average(random time sample N*T) = (N-1)*T
Deriving Exponential Distribution for PoW solvetimes
If the target is 1/1000th of 2^256, then each hash has a 1/1000 chance of being below the target. The p of a hash not that low is 1-1/1000 which means the p of not succeeding in a sequence of n hashes is (1-1/1000)^n. This can be rewritten as
p = (1 - 1/1000*n/n)^n (1)
For large n, the following is true:
p = (1 - c/n)^n = e^(-c)
We can use c = t * HR * target / 2^256 because 1/1000 comes from 2^256/target and n = number of hashes = HR * t. So :
p = e^(- HR * t * target/2^256) (2)
Let λ = HR * target/2^256
p = e^(-t*λ)
CDF = 1- p = 1 - e^(-t*λ)
PDF = d(CDF)/dt = λ*e^(-t*λ)
p is the probability a block will arrive after time t, so the 1-p=CDF is the probability it will arrive by t. The CDF is for a Exponential distribution. p = 1-e^(-t * λ) is commonly seen in engineering and nature because it is the fraction of something that is blocked in time or space for a blocking rate of λ per distance or time (in same units as t). A larger hashrate blocks solves from taking longer.
[update in 2022: The following is difficult even for me to follow. I'm sure there's a much better way to present it.]
Derivation of a Difficulty Algorithm
A common way to express a difficulty algorithm that's needed to get avg solvetime = T is to skip most of the following and say
next_target = previous_target * λ_desired / λ_observed
or
next_target = previous_target * HR_expected / HR_observed
which is the same as eq 3 below when replacing HR with λ_observed * 2^256 / previous_target.
To derive a difficulty algorithm, our goal is to set a target that will result in an avg solvetime of T. We do this by applying the expected value integral to the PDF and setting it equal to T. This gives λ = 1/T = HR*target/2^256. Rearranging shows how we should set the target:
next_target = 2^256 / (HR*T) (3)
We need to estimate HR from previous target(s) and solvetime(s), but we need to be careful because the expected value equation is for all possible solvetimes t which we will see only in an infinite number of samples. We can't simply say HR = 2^256 / t / prev_target for a 1-block estimate. It's technically impossible to estimate HR from 1 sample (see below). More generally, we can't use HR = 2^256 / sum_t / sum_target because there is a finite number of samples. It's approximately correct for a large number of samples, if the target is not changing.
In a difficulty algorithm like this:
next_target = prev_target * λ_desired / λ_measured = prev_target * avg(t) / T
the avg(t) will be too small if our sample size is small. To correct for the error, use:
1/λ_measured = avg(t) * N / (N-1)
The math shows an infinity at N=1. But if no solvetimes are < 1 and there are integer solvetiems with T=600,
1/λ_measured = avg(t) * 6.5
For N=2, the correction factor is 2. See the last section how this seems to be related to the memoryless property. That is, picking the start of a block to start a timer is the same as picking a random point in time. If you pick a random point in time, the current block began T in the past and the next block will occur in T. This means a randomly chosen block will take on average 2*T due to slow solves canceling the effect of fast solves.
The solvetime for a block is determined by setting rand() = 1-CDF = x and solving for t in the following:
1-CDF = x = e^(-t*HR*target/2^256)
t = -ln(x) * 2^256 / (HR * target) (5)
This entire issue is based on avg(1/y) != 1/avg(y). When we apply a HR adjustment to the target many times in a row, we're applying avg_many( 1 / avg_N(-ln(x))) which equals N/(N-1). A simple way to show this is correct for N=2 is to run the experiment or do a definite double integral of 1/[(-ln(x)-ln(y)/2] for x and y, both 0 to 1. So BTC-type difficulty algorithms (a fixed target for N blocks and adjusting only once per N blocks) require a modification to eq 3.
next_target = prev_target * timespan/N / T * N/(N-1) (8)
BTW, more complex difficulty algorithms can change the target during the block based on the timestamp in the header. The correction factor can again be determined by using eq 5 where HR and target can be functions of t, then solve for t again to isolate the ln(x) function then integrate that from 0 to 1. This is the same as using the expectation integral on t*PDF from 0 to infinity because x is equally probable for all t's from 0 to 1.
Calculating Hashrate in General
As discussed above, if difficulty or target are constant:
HR = priorD / avg(t) * (N-1)/N
HR = 2^256/priorTarget / avg(t) * (N-1)/N
If D or target change every block, the following is more accurate for determining hashrate, but the (N-1)/N correction should not be used in simple moving average difficulty algorithms because the N samples overlap when you're adjusting every block, so they're not independent sample. I tried [(N-1)/N]^(1/N) to account for this but it was not accurate for smallish N.
HR = harmonicMeanD / avg(t) * (N-1)/N
HR = 2^256/avgTarget / avg(t) * (N-1)/N
The harmonic mean of D is used because of another problem caused by avg(1/x) != 1/avg(x). D = 2^256/target, but avgD != 2^256/target. You can show that
harmonicMeanD = 2^256/avgTarget
A declarative, efficient, and flexible JavaScript library for building user interfaces.
🖖 Vue.js is a progressive, incrementally-adoptable JavaScript framework for building UI on the web.
TypeScript is a superset of JavaScript that compiles to clean JavaScript output.
An Open Source Machine Learning Framework for Everyone
The Web framework for perfectionists with deadlines.
A PHP framework for web artisans
Bring data to life with SVG, Canvas and HTML. 📊📈🎉
JavaScript (JS) is a lightweight interpreted programming language with first-class functions.
Some thing interesting about web. New door for the world.
A server is a program made to process requests and deliver data to clients.
Machine learning is a way of modeling and interpreting data that allows a piece of software to respond intelligently.
Some thing interesting about visualization, use data art
Some thing interesting about game, make everyone happy.
We are working to build community through open source technology. NB: members must have two-factor auth.
Open source projects and samples from Microsoft.
Google ❤️ Open Source for everyone.
Alibaba Open Source for everyone
Data-Driven Documents codes.
China tencent open source team.